题目内容
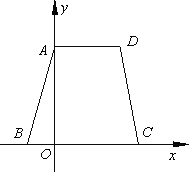
如下图：等腰梯形ABCD按照如下方法折叠后（AD正好落在边BC上）得梯形EBCF，且EF=2FC=8cm．则原梯形ABCD的周长是（ ）
| A、16cm | B、32cm | C、24cm | D、40cm |
分析：根据题意可判断出EF是原梯形的中位线，由此可得AD+BC的长度，再根据EF=2FC=8cm即可得出原梯形ABCD的周长．
解答：解：由题意得：∵AD正好落在边BC上，
∴可得：EF是原梯形的中位线，
∴AD+BC=2EF=16，
又FC=
DC=
AB，
∴原梯形ABCD的周长=AD+BC+AB+DC=32．
故选B．
∴可得：EF是原梯形的中位线，
∴AD+BC=2EF=16，
又FC=
| 1 |
| 2 |
| 1 |
| 2 |
∴原梯形ABCD的周长=AD+BC+AB+DC=32．
故选B．
点评：本题考查等腰梯形的性质，比较简单，关键是根据题意判断出EF是原梯形的中位线．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
．
？若存在，请求出该点坐标，若不存在，请说明理由．
，则梯形ABCD的周长为（ ）
B．
C．
D．