Question

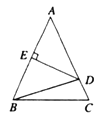
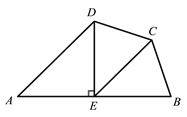
【题目】如图，在四边形中，，，是边的垂直平分线，连接．

（1）求证：；

（2）若，，求的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】分析：（1）由线段垂直平分线的性质得到AE=EB=4，再由∠A=45°，得到DE=AE=EB，由“SSS”公理即可得到△EDC≌△EBC，由全等三角形对应角相等即可得出结论；

（2）过点C作CH⊥AB于点H，即可得到CH=EH．设EH=x，则BH=4-x．在Rt△CHB中，由勾股定理可求出x的值，由CE=EH即可得到结论．

详解：（1）∵是边的垂直平分线，

∴，

∵，

∴，

又∵，

∴△≌△．

∴．

（2）过点作于点，可得：，

设，则，

在中，，

即，

解得：（不合题意，舍去），

即．

∴．