题目内容
 如图线段AB在x轴上,以AB为直径的圆交y轴于点C,己知AC=2
如图线段AB在x轴上,以AB为直径的圆交y轴于点C,己知AC=2 ,BC=
,BC= .
.
(1)求点A、B、C三点的坐标;
(2)设过A、B、C三点的抛物线的顶点为D,求四边形ABCD的面积:
(3)求该抛物线与圆的另一个交点坐标.
解:(1)因为AB为直径,所以∠ACB=90°,
在直角三角形ABC中,AB= =
=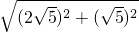 =5,
=5,
∵△BOC∽△BCA,
∴ =
= ,
,
∴BO= =
= =1,AO=4,
=1,AO=4,
又∵△AOC∽△COB,
 =
=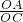 ,
,
即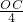 =
= ,
,
解得OC=2,
由此可知点A、B、C三点的坐标分别为(-4,0),(1,0),(0,2);
(2)设抛物线解析式为y=ax2+bx+c,把A、B、C三点代入解析式得,
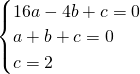 ,
,
解得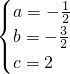 ,
,
所以函数解析式为y=- x2-
x2- x+2,
x+2,
顶点坐标D为(- ,
, );
);
过点D作DE垂直于AB,垂足为E,如图:
S四边形ABCD=S△ADE+S梯形CDEO+S△BOC,
= ×(4-
×(4- )×
)× +
+ ×(
×( +2)×
+2)× +
+ ×1×2,
×1×2,
=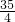 ;
;
(3)由上图可知,抛物线与圆的另一个交点F与点C是对称点,
所以点F的坐标为(-3,2).
分析:(1)利用勾股定理和三角形相似的性质解决问题;
(2)求出函数解析式,得出顶点坐标,分割图形,利用梯形的面积与三角形的面积即可解答问题;
(3)利用二次函数图象上点的对成性解答即可.
点评:此题综合考查了勾股定理,三角形相似的性质,组合图形的面积,二次函数对称性,以及待定系数法球函数解析式.
在直角三角形ABC中,AB=
 =
=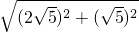 =5,
=5,∵△BOC∽△BCA,
∴
 =
= ,
,∴BO=
 =
= =1,AO=4,
=1,AO=4,又∵△AOC∽△COB,
 =
=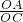 ,
,即
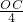 =
= ,
,解得OC=2,
由此可知点A、B、C三点的坐标分别为(-4,0),(1,0),(0,2);
(2)设抛物线解析式为y=ax2+bx+c,把A、B、C三点代入解析式得,
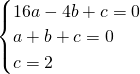 ,
,解得
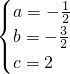 ,
,
所以函数解析式为y=-
 x2-
x2- x+2,
x+2,顶点坐标D为(-
 ,
, );
);过点D作DE垂直于AB,垂足为E,如图:
S四边形ABCD=S△ADE+S梯形CDEO+S△BOC,
=
 ×(4-
×(4- )×
)× +
+ ×(
×( +2)×
+2)× +
+ ×1×2,
×1×2,=
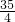 ;
;(3)由上图可知,抛物线与圆的另一个交点F与点C是对称点,
所以点F的坐标为(-3,2).
分析:(1)利用勾股定理和三角形相似的性质解决问题;
(2)求出函数解析式,得出顶点坐标,分割图形,利用梯形的面积与三角形的面积即可解答问题;
(3)利用二次函数图象上点的对成性解答即可.
点评:此题综合考查了勾股定理,三角形相似的性质,组合图形的面积,二次函数对称性,以及待定系数法球函数解析式.

练习册系列答案
相关题目
 如图线段AB在x轴上,以AB为直径的圆交y轴于点C,己知AC=2
如图线段AB在x轴上,以AB为直径的圆交y轴于点C,己知AC=2 ,BC=
,BC= .
.

 ;
; ,若存在,求出点P的坐标;若不存在,试说明理由。
,若存在,求出点P的坐标;若不存在,试说明理由。
 的值不变,其中只有一个结论是正确的,请你找出这个结论,并加以说明。
的值不变,其中只有一个结论是正确的,请你找出这个结论,并加以说明。