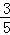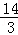题目内容
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

(1)12m或16m;(2)195.
【解析】
试题分析:(1)方程的应用解题关键是找出等量关系,列出方程求解. 本题等量关系为:矩形的面积为192.
(2)由在P处有一棵树与墙CD,AD的距离分别是15m和6m,求出x的取值范围,根据二次的性质求解即可.
试题解析:(1)∵AB=xm,∴BC= .
.
根据题意,得 ,解得
,解得 或
或 .
.
∴x的值为12m或16m.
(2)∵根据题意,得 ,∴
,∴ .
.
∵ ,∴当
,∴当 时,S随x的增大而增大.
时,S随x的增大而增大.
∴当 时,花园面积S最大,最大值为
时,花园面积S最大,最大值为 .
.
考点:1.方程的应用(几何问题);2.二次函数的应用(实际问题);3.不等式的应用.

为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了依次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
各组人数统计表
组号 | 年龄分组 | 频数(人) | 频率 |
第一组 | 20≤x<25 | 50 | 0.05 |
第二组 | 25≤x<30 | a | 0.35 |
第三组 | 35≤x<35 | 300 | 0.3 |
第四组 | 35≤x<40 | 200 | b |
第五组 | 40≤x≤45 | 100 | 0.1 |
(1)求本次调查的样本容量及表中的a、b的值;
(2)调查结果得到对生产和居住环境满意的人数的频率分布直方图如图,政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
(3)从第二张和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.