题目内容
如图,反比例函数y1=| k | x |
 B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.
B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.(1)当y2>y1时,x的取值范围;
(2)求出y1和y3的关系式.
分析:(1)观察函数图象,取反比例函数图象位于正比例函数图象下方时对应的x的取值范围即可,(2)根据三角形OBC的面积为2
可以求出B点的坐标,再把B点坐标代入即可求出y1和y3的关系式
可以求出B点的坐标,再把B点坐标代入即可求出y1和y3的关系式
解答:解:(1)观察图象可知:反比例函数y1=
(x>0)与正比例函数y2=mx交点的横坐标为x=1,
若y2>y1,则x>1,
(2)解:∵△OBC的面积为2,
∴点B坐标为(2,2),
将B(2,2)代入y1=
,得:k=4,
将B(2,2)代入y3=nx,得:n=1,
∴y1=
,y3=x.
| k |
| x |
若y2>y1,则x>1,
(2)解:∵△OBC的面积为2,
∴点B坐标为(2,2),
将B(2,2)代入y1=
| k |
| x |
将B(2,2)代入y3=nx,得:n=1,
∴y1=
| 4 |
| x |
点评:本题主要考查反比例函数与一次函数的交点问题和反比例函数图象上点的坐标特征的知识点,解答本题的突破口是根据三角形的面积公式求出B点的坐标,解答本题要熟练掌握反比例函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
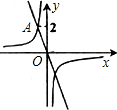 如图,反比例函数y1=
如图,反比例函数y1=| k |
| x |
| A、-2<X<2 |
| B、-1<x<0或x>1 |
| C、x<-1或0<x<1 |
| D、x<-1或x>1 |
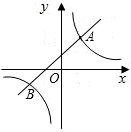 如图,反比例函数
如图,反比例函数 (2012•滦南县一模)如图,反比例函数
(2012•滦南县一模)如图,反比例函数 已知如图:反比例函数
已知如图:反比例函数 如图,反比例函数y1=
如图,反比例函数y1=