Question

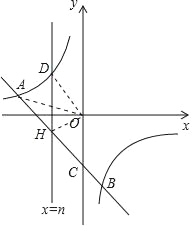
【题目】如图，已知直线l：y=ax+b与反比例函数y=﹣的图象交于A（﹣4，1）、B（m，﹣4），且直线l与y轴交于点C．

（1）求直线l的解析式；

（2）若不等式ax+b＞﹣成立，则x的取值范围是　 　；

（3）若直线x=n（n＜0）与y轴平行，且与双曲线交于点D，与直线l交于点H，连接OD、OH、OA，当△ODH的面积是△OAC面积的一半时，求n的值．

Answer 1

【答案】（1）y=﹣x﹣3；（2）x＜﹣4或0＜x＜1；（3）n的值为﹣1，﹣2，﹣5．

【解析】分析：(1)由点B在反比例函数的图象上求m的值，用待定系数法求直线l的解析式；(2)即直线在曲线的上方时x的取值范围；(3)求出点C的坐标，确定△OAC的面积，用含n的式子表示出DH的长，分两种情况，根据三角形的面积公式列方程求解.

详解：解：(1)∵y＝﹣，B(m，﹣4)，

∴m＝1，∴B(1，﹣4)．

∵y＝ax＋b过A(﹣4，1)，B(1，﹣4)，

∴，

解得，

∴直线解析式为y＝﹣x﹣3；

(2)由函数图象可知，不等式ax＋b＞﹣成立，则x的取值范围是x＜﹣4或0＜x＜1．

故答案是：x＜﹣4或0＜x＜1；

(3)∵直线与y轴交点为(0，﹣3)，

∴S△OAC＝×3×4＝6.

由直线x＝n可知D(n，﹣)，H(n，－n－3)，

当﹣4＜n＜0时，DH＝－－(－n－3)＝－n＋3，

∵，S△ODH＝S△OAC＝×6＝3，

∴·(－n)＝3，即(－)(－n)＝3.

整理得n2＋3n＋2＝0，

解得：n1＝﹣1，n2＝﹣2；

当n＜﹣4时，DH＝(－n－3)－(－)＝－n－3，

∴·(－n)＝3，即(－n－3)(－n)＝3.

整理得n2＋3n﹣10＝0，

解得：n1＝﹣5，n2＝2(不合题意，舍去)．

综上可知n的值为﹣1，﹣2，﹣5．