Question

如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=AB=1，BC=2．将点A折叠到CD边上，记折叠后A点对应的点为P（P与D点不重合），折痕EF只与边AD、BC相交，交点分别为E、F．过P作PN∥BC交AB于N、交EF于M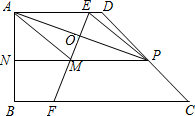，连接PA、PE、AM，EF与PA相交于O．
（1）指出四边形PEAM的形状（不需证明）；
（2）记∠EPM=a，△AOM、△AMN的面积分别为S₁、S₂．
①求证：

S1

tan a 2

=

1

8

PA2；
②设AN=x，y=

S1-S2

tan a 2

，试求出以x为自变量的函数y的解析式，并确定y的取值范围．

Answer 1

分析：（1）根据题意，结合菱形的判定定理即可推出四边形AMPE为菱形，
（2）①四边形AMPE为菱形，即可得：∠MAP=

1

2

α，S₁=

1

2

OA•OM，OA=

1

2

PA，又由在Rt△AOM中，tan

α

2

=

OM

OA

，求得OM=OA•tan

α

2

；则可得

S1

tan a 2

=

1

8

PA2；
②首先过点D作DH⊥BC于H，则DK⊥PN，BH=AB=AD=DH=1，DK=AN=x，求得PN=1+x，在Rt△ANP中，由AP²=AN²+PN²，可求得AP²的值，然后过E作PM⊥EG于G，令△EGM的面积为S，由△EGM∽△AOM，即可得S=

4x2

AP2

S₁，则问题得解．

解答：解：（1）答案为：菱形；

（2）①证明：
∵四边形AMPE为菱形，
∴∠MAP=

1

2

α，S₁=

1

2

OA•OM，OA=

1

2

PA，
∵在Rt△AOM中，tan

α

2

=

OM

OA

，
∴OM=OA•tan

α

2

；
∴S₁=

1

2

OA•OM=

1

2

×

1

2

PA×

1

2

PA•tan

α

2

=

1

8

PA²•tan

α

2

∴

S1

tan a 2

=

1

8

PA2；
②过点D作DH⊥BC于H，交PN于K．
则：DK⊥PN，BH=AB=AD=DH=1，DK=AN=x，
∵CH=BC-BH=2-1=1，
∴CH=DH，
∴PK=DK=x，
∴PN=1+x，
在Rt△ANP中，
AP²=AN²+PN²=x²+（1+x）²=2x²+2x+1．
过E作EG⊥PM于G，令△EGM的面积为S，
∵△EGM∽△AOM，
∴

S

S1

=(

EG

AO

)2=

x2

1 4 AP2

=

4x2

AP2

，
则S=

4x2

AP2

S₁，
∵△AOE由△POE折叠而成，
∴AE=PE，AP⊥EM，
∵四边形AMPE是菱形，
∴AN=DK=x，
如图，当E与D重合时，
∵PN=1+x，AN=x，AM=AD=PM=PD=1，
∴MN=PN-PM=1+x-1=x，
∴AN=MN，
在Rt△AMN中，AN²+MN²=AM²，
∴x²+x²=1²，
∴x=

2

2

，
∴0＜x＜

2

2

，
∵四边形ANGE的面积等于菱形AMPE的面积，
∴4S₁=2S₁+S₂+S，即2S₁=S₂+S，
∴S₁-S₂=S-S₁=

4x2

AP2

S₁-S₁=（

4x2

AP2

-1）S₁，
∴y=

S1-S2

tan α 2

=（

4x2

AP2

-1）×

S1

tan α 2

=（

4x2

AP2

-1）×

1

8

AP²=

1

8

（4x²-AP²），
∴y=

1

4

x²-

1

4

x-

1

8

（-

3

16

≤y＜-

1

8

）．

点评：此题考查了相似三角形的判定与性质，菱形的性质，三角函数的性质以及二次函数的知识．此题综合性很强，难度较大，解题的关键是方程思想与数形结合思想的应用．