题目内容
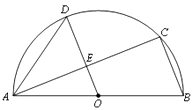
【题目】如图，∠ACB=∠ECD=90°，AC=BC，EC=DC，点D在AB边上．
（1）求证：△ACE≌△BCD．
（2）若AE=3，AD=2．求ED的长．
【答案】（1）见解析；（2）
【解析】
试题分析：（1）根据∠ACB=∠ECD=90°求出∠DCB=∠ECA，根据SAS推出两三角形全等即可；
（2）根据等腰直角三角形求出∠BAC=∠B=45°，根据全等三角形的性质求出∠EAC=∠B=45°，求出∠EAD=90°，根据勾股定理求出即可．
【解答】（1）证明：∵∠ACB=∠ECD=90°，
∴∠ACB﹣∠ACD=∠ECD﹣∠ACD，
∴∠DCB=∠ECA，
在△ACE和△BCD中
∴△ACE≌△BCD（SAS）；
（2）解：∵∠ACB=90°，AC=BC，
∴∠BAC=∠B=45°，
∵△ACE≌△BCD，
∴∠EAC=∠B=45°，
∴∠EAD=90°，
∴在Rt△AED中，∠EAD=90°，AE=3，AD=2，由勾股定理得：ED=
=．
【题目】“端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
设某位顾客购买了x元的该种粽子．
（1）补充表格，填写在“横线”上：
（2）列式计算说明，如果顾客在“端午节”当天购买该种粽子超过200元，那么到哪家超市花费更少？
x （单位：元） | 实际在甲超市的花费 （单位：元） | 实际在乙超市的花费 （单位：元） |
0＜x≤200 | x | x |
200＜x≤300 | x | |
x＞300 |
【题目】为响应国家节能减排的号召，鼓励居民节约用电，各省市先后出台了居民用电“阶梯价格”制度，下表是某市的电价标准（每月）．
阶梯 | 一户居民每月用电量x（单位：度） | 电费价格（单位：元/度） |
一档 | 0＜x≤180 | a |
二档 | 180＜x≤280 | b |
三档 | x＞280 | 0.82 |
（1）已知小华家四月份用电200度，缴纳电费105元；五月份用电230度，缴纳电费122.1元，请你根据以上数据，求出表格中a，b的值；
（2）六月份是用电高峰期，小华家计划六月份电费支出不超过208元，那么小华家六月份最多可用电多少度？
