题目内容
 用尺规作一个角的角平分线的示意图如下,作法是:以O为圆心作一圆弧交角的两边于A、B两点;再分别以A、B两点为圆心,以大于
用尺规作一个角的角平分线的示意图如下,作法是:以O为圆心作一圆弧交角的两边于A、B两点;再分别以A、B两点为圆心,以大于| 1 |
| 2 |
分析:根据作图过程可知AO=BO,AP=BP,再有公共边OP=OP,可利用SSS定理证明△OAP≌△OBP.
解答:解:在△OAP和△OBP中,
,
∴△OAP≌△OBP(SSS),
故选:A.
|
∴△OAP≌△OBP(SSS),
故选:A.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.

⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
⑵如图3,⊙ 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).
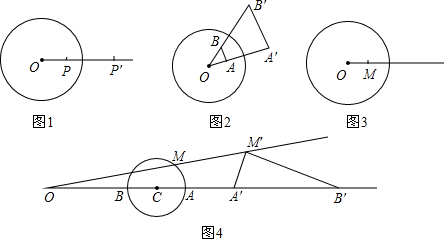
⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
(12分)如图1,在平面上,给定了半径为 的⊙
的⊙ ,对于任意点
,对于任意点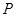 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点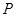 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点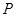 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
⑴如图2,⊙ 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )
A.∠ | B.∠ | C.∠ | D.∠ |
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).⑶如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.已知基圆
 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.

 (C)∠
(C)∠ (D)∠
(D)∠
 =90°.
=90°.
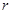 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 =
= ,这种把点
,这种把点
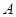 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ (C)∠
(C)∠ (D)∠
(D)∠ ,请用尺规作图画出点
,请用尺规作图画出点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法). 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ =90°.
=90°.