Question

如图，在Rt△ABC中，∠C=90°，Rt△BAP中，∠BAP=90°，已知∠CBO=∠ABP，BP交AC于点O，E为AC上一点，且AE=OC．

（1）求证：AP=AO；

（2）求证：PE⊥AO；

（3）当AE=AC，AB=10时，求线段BO的长度．

 

 

Answer 1

（1）证明见解析；

（2）证明见解析；

（3）BO=．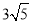

【解析】

试题分析：（1）根据等角的余角相等证明即可；

（2）过点O作OD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CO=DO，利用“SAS”证明△APE和△OAD全等，根据全等三角形对应角相等可得∠AEP=∠ADO=90°，从而得证；

（3）设C0=3k，AC=8k，表示出AE=CO=3k，AO=AP=5k，然后利用勾股定理列式求出PE=4k，BC=BD=10﹣4k，再根据相似三角形对应边成比例列式求出k=1然后在Rt△BDO中，利用勾股定理列式求解即可．

试题解析：（1）∵∠C=90°，∠BAP=90°

∴∠CBO+∠BOC=90°，∠ABP+∠APB=90°，

又∵∠CBO=∠ABP，

∴∠BOC=∠ABP，

∵∠BOC=∠AOP，

∴∠AOP=∠ABP，

∴AP=AO；

（2）如图，过点O作OD⊥AB于D，

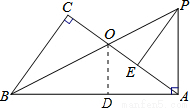
∵∠CBO=∠ABP，

∴CO=DO，

∵AE=OC，

∴AE=OD，

∵∠AOD+∠OAD=90°，∠PAE+∠OAD=90°，

∴∠AOD=∠PAE，

在△AOD和△PAE中，

∵AE＝OD，∠AOD＝∠PAE，AP＝AO，

∴△AOD≌△PAE（SAS），

∴∠AEP=∠ADO=90°

∴PE⊥AO；

（3）设AE=OC=3k，

∵AE=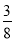AC，∴AC=8k，

∴OE=AC﹣AE﹣OC=2k，

∴OA=OE+AE=5k．

由（1）可知，AP=AO=5k．

如图，过点O作OD⊥AB于点D，

∵∠CBO=∠ABP，∴OD=OC=3k．

在Rt△AOD中，AD=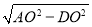==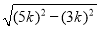4k．

∴BD=AB﹣AD=10﹣4k．

∵OD∥AP，

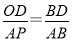∴，即

，

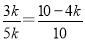∵AB=10，PE=AD，

∴PE=AD=4K，BD=AB﹣AD=10﹣4k，

由∠CBO=∠ABP，根据轴对称BC=BD=10﹣4k，

∵∠BOC=∠EOP，∠C=∠PEO=90°，

∴△BCO∽△PEO，

∴，

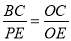即 ，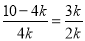

解得k=1．

∴BD=10﹣4k=6，OD=3k=3，

在Rt△BDO中，由勾股定理得：

BO=．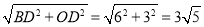

考点：1.相似三角形的判定与性质2.全等三角形的判定与性质3.角平分线的性质4.等腰三角形的判定与性质．