Question

某园林为保护年久倾斜的古树，用一根木棍加以支撑，如图1所示，图2是其示意图，已知∠B=60°，∠ACB=45°，BC=10m，求支撑点A距地面的高度．

Answer 1

解：过点A作AD⊥BC于点D，
设AD=xm，
在Rt△ABD中，∠ACB=45°，
∴∠DAC=45°=∠ACB，
∴AD=DC=x，
∵在Rt△ADC中，∠ADB=90°，∠B=60°，
cot60°=，
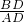∴BD=ADcot60°=x，
∴BD
由题意BC=BD+CD=10m，
∴x+x=10，
x=15-5，
∴AD=（15-5）m；
答：点A到地面的距离为（15-5）m．
分析：过A作BC的垂线AD，设AD=xm，可分别在Rt△ABD、Rt△ACD中，利用AD表示出BD、CD的长，然后根据BC的长来求得AD的值．
点评：此题主要考查的是姐直角三角形的应用，熟练掌握直角三角形的边角关系是解题的关键．