题目内容
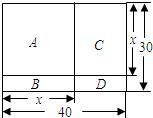
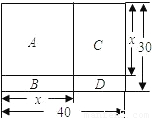
现有一块矩形场地,如下图所示,长为
40 m,宽为30 m,要将这块场地划分为四块分别种植:A.兰花;B.菊花;C.月季;D.牵牛花.
(1)求出这块场地中种植菊花的面积y与B场地的长x之间的函数关系式;求出此函数与x轴的交点坐标,并写出自变量的取值范围;
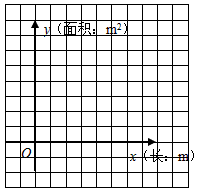
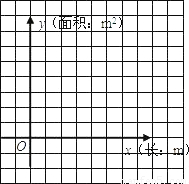
(2)当x是多少时,种植菊花的面积最大?最大面积是多少?请在下图中画出此函数图象的草图(提示:找三点描出图象即可).

答案:
解析:
解析:
|
解: (1)由题意知,B场地宽为(30-x)m,所以y=x(30-x)=-x2+30x.当 y=0时,即-x2+30x=0,解得x1=0,x2=30.所以函数图象与 x轴的交点坐标为(0,0),(30,0);自变量x的取值范围为0<x<30.(2)因为y=-x2+30x=-(x-15)2+225,所以当x=15 m时,种植菊花的面积最大,最大面积为225 m2.草图如图所示.
点评:利用二次函数解决实际问题时,需结合函数的草图进行分析,这样可以对解答过程进行检验. |

练习册系列答案
相关题目

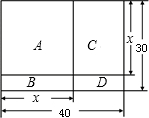 兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.
兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.