题目内容
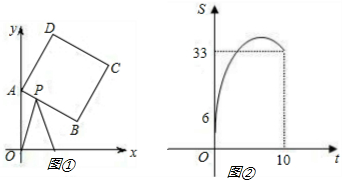
正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立���写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

解答:
解:(1)AP=EF,AP⊥EF,理由如下:
连接AC,则AC必过点O,延长FO交AB于M;
∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,
∴四边形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE,
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
(2)题(1)的结论仍然成立,理由如下:
延长AP交BC于N,延长FP交AB于M;
∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB﹣BM=AM,BC﹣BE=EC=PF,且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE,
∴AP=EF,∠APM=∠FPN=∠PEF
∵∠PEF+∠PFE=90°,∠FPN=∠PEF,
∴∠FPN+∠PFE=90°,即AP⊥EF,
故AP=EF,且AP⊥EF.
(3)题(1)(2)的结论仍然成立;
如右图,延长AB交PF于H,证法与(2)完全相同.



练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 17、已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为
17、已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为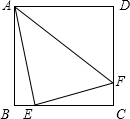 如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于
如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于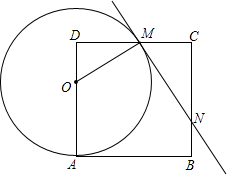 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.