题目内容
 如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知OA=
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知OA= ,AB=1,则点A1的坐标是
,AB=1,则点A1的坐标是
- A.(
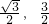 )
) - B.(
 )
) - C.(
 )
) - D.(
 )
)
A
分析:根据折叠的性质,OA=OA1,∠AOB=∠A1OB,从而求出∠A1OD,利用三角函数求出OD、A1D即可解答.
解答: 解:在Rt△AOB中,tan∠AOB=
解:在Rt△AOB中,tan∠AOB= ,
,
∴∠AOB=30°.
而Rt△AOB≌Rt△A1OB,
∴∠A1OB=∠AOB=30°.
作A1D⊥OA,垂足为D,如图所示.
在Rt△A1OD中,OA1=OA= ,∠A1OD=60°,
,∠A1OD=60°,
∵sin∠A1OD= ,
,
∴A1D=OA1•sin∠A1OD=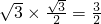 .
.
又cos∠A1OD= ,
,
∴OD=OA1•cos∠A1OD=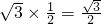 .
.
∴点A1的坐标是 .
.
故选A.
点评:此题主要考查图形对折的特征及点的坐标的求法.
分析:根据折叠的性质,OA=OA1,∠AOB=∠A1OB,从而求出∠A1OD,利用三角函数求出OD、A1D即可解答.
解答:
 解:在Rt△AOB中,tan∠AOB=
解:在Rt△AOB中,tan∠AOB= ,
,∴∠AOB=30°.
而Rt△AOB≌Rt△A1OB,
∴∠A1OB=∠AOB=30°.
作A1D⊥OA,垂足为D,如图所示.
在Rt△A1OD中,OA1=OA=
 ,∠A1OD=60°,
,∠A1OD=60°,∵sin∠A1OD=
 ,
,∴A1D=OA1•sin∠A1OD=
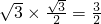 .
.又cos∠A1OD=
 ,
,∴OD=OA1•cos∠A1OD=
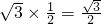 .
.∴点A1的坐标是
 .
.故选A.
点评:此题主要考查图形对折的特征及点的坐标的求法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: