题目内容
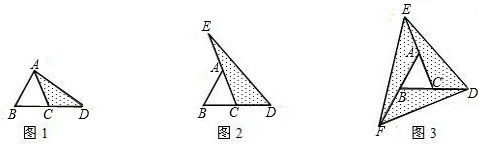
如图1至图3是将正方体截去一部分后得到的多面体．
（1）根据要求填写表格：
（2）猜想f、v、e三个数量间有何关系；
（3）根据猜想计算，若一个多面体有顶点数2013个，棱数4023条，试求出它的面数．
（1）根据要求填写表格：
| 面数（f） | 顶点数（v） | 棱数（e） | |
| 图1 | 7 7 |
9 9 |
14 14 |
| 图2 | 6 6 |
8 8 |
12 12 |
| 图3 | 6 6 |
10 10 |
14 14 |
（3）根据猜想计算，若一个多面体有顶点数2013个，棱数4023条，试求出它的面数．
分析：（1）根据图形数出即可．
（2）根据（1）中结果得出f+v-e=2．
（3）代入f+v-e=2求出即可．
（2）根据（1）中结果得出f+v-e=2．
（3）代入f+v-e=2求出即可．
解答：解：（1）题1，面数f=7，顶点数v=9，棱数e=14，
题2，面数f=6，顶点数v=8，棱数e=12，
题3，面数f=6，顶点数v=10，棱数e=14，
故答案为：7，9，14.6，8，12，6，10，14．
（2）f+v-e=2．
（3）∵v=2013，e=4023，f+v-e=2
∴f+2013-4023=2，
f=2012，
即它的面数是2012．
题2，面数f=6，顶点数v=8，棱数e=12，
题3，面数f=6，顶点数v=10，棱数e=14，
故答案为：7，9，14.6，8，12，6，10，14．
（2）f+v-e=2．
（3）∵v=2013，e=4023，f+v-e=2
∴f+2013-4023=2，
f=2012，
即它的面数是2012．
点评：本题考查了截一个几何体，图形的变化类的应用，关键是能根据（1）中的结果得出规律．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图1至图3是将正方体截去一部分后得到的多面体．
（1）根据要求填写表格：
| 面数（f） | 顶点数（v） | 棱数（e） | |
| 图1 | ______ | ______ | ______ |
| 图2 | ______ | ______ | ______ |
| 图3 | ______ | ______ | ______ |
（2）猜想f、v、e三个数量间有何关系；
（3）根据猜想计算，若一个多面体有顶点数2013个，棱数4023条，试求出它的面数．