题目内容
如图，A、O、B在同一直线上，OE平分∠BOC，OF平分∠AOC，则∠AOF+∠BOE
=________度．
90
分析：首先根据角平分线定义可得∠AOF=
∠AOC，∠EOB=∠COB，再根据∠AOC+∠BOC=180°，可得答案．
解答：∵OE平分∠BOC，OF平分∠AOC，
∴∠AOF=∠AOC，∠EOB=∠COB，
∵∠AOC+∠BOC=180°，
∴∠AOF+∠BOE=
=×180°=90°，
故答案为：90．
点评：此题主要考查了角平分线的定义，以及邻补角，关键是理清角之间的关系．
分析：首先根据角平分线定义可得∠AOF=
∠AOC，∠EOB=∠COB，再根据∠AOC+∠BOC=180°，可得答案．解答：∵OE平分∠BOC，OF平分∠AOC，
∴∠AOF=
∠AOC，∠EOB=∠COB，∵∠AOC+∠BOC=180°，
∴∠AOF+∠BOE=
=×180°=90°，故答案为：90．
点评：此题主要考查了角平分线的定义，以及邻补角，关键是理清角之间的关系．
练习册系列答案
相关题目
19、如图，以△ABC三边为边在BC同侧作三个等边△ABD、△BCE、△ACF．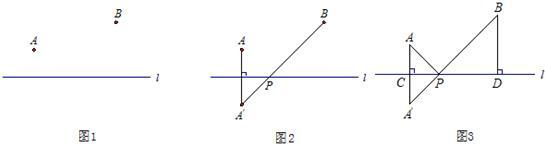
28、已知：如图，△ABC和△DBC的顶点在BC边的同侧，AB=DC，AC=BD交于E，∠BEC的平分线交BC于O，延长EO到F，使EO=OF．求证：四边形BFCE是菱形．
已知：如图，点A和点B在直线l同一侧．求作：直线l上一点P，使PA+PB的值最小．