题目内容
 如图,在△ABC,D、E、F分别是边BC,AB,CA的中点,则图中平行四边形的个数为
如图,在△ABC,D、E、F分别是边BC,AB,CA的中点,则图中平行四边形的个数为
- A.1
- B.2
- C.3
- D.4
C
分析:由于D、E、F分别是边BC,AB,CA的中点,易知DE、DF、EF都是△ABC的中位线,那么DE∥AC,DF∥AB,EF∥BC,根据平行四边形的定义,两两结合易证四边形EDCF是平行四边形;四边形EBDF是平行四边形;四边形AEDF是平行四边形.
解答:3个.
∵D、E、F分别是边BC,AB,CA的中点,
∴DE、DF、EF都是△ABC的中位线,
∴DE∥AC,DF∥AB,EF∥BC,
∴四边形EDCF是平行四边形,
四边形EBDF是平行四边形,
四边形AEDF是平行四边形.
故选C.
点评:本题考查了平行四边形的判定、三角形中位线定理,解题的关键是熟练掌握三角形中位线定理的内容.
分析:由于D、E、F分别是边BC,AB,CA的中点,易知DE、DF、EF都是△ABC的中位线,那么DE∥AC,DF∥AB,EF∥BC,根据平行四边形的定义,两两结合易证四边形EDCF是平行四边形;四边形EBDF是平行四边形;四边形AEDF是平行四边形.
解答:3个.

∵D、E、F分别是边BC,AB,CA的中点,
∴DE、DF、EF都是△ABC的中位线,
∴DE∥AC,DF∥AB,EF∥BC,
∴四边形EDCF是平行四边形,
四边形EBDF是平行四边形,
四边形AEDF是平行四边形.
故选C.
点评:本题考查了平行四边形的判定、三角形中位线定理,解题的关键是熟练掌握三角形中位线定理的内容.

练习册系列答案
相关题目
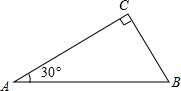 的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.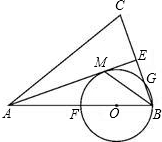 F,FB恰为⊙O的直径.
F,FB恰为⊙O的直径. 7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=
7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=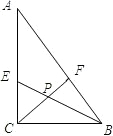 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为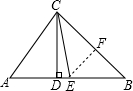 如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为
如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为