题目内容
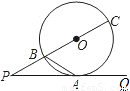
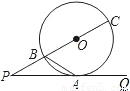
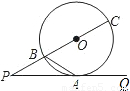
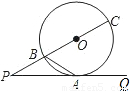
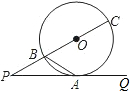如图，射线PQ是⊙O相切于点A，射线PO与⊙O相交于B，C两点，连接AB，若PB：BC=1：2上，则∠PAB的度数等于（ ）| A、26° | B、30° | C、32° | D、45° |
分析：根据切割线定理，切线的性质，直角三角形的性质计算．
解答：
解：连接OA，则有OA⊥PA，
由于PB：BC=1：2，
∴设BC=2x，
则PB=OB=OA=x，PC=3x，
由切割线定理知，PA2=PB•PC=3x2，
∴PA=
x，
tan∠P=OA：PA=1：
，
∴∠P=30°，
∴∠AOB=90°-∠P=90°-30°=60°，
∴△AOB是等边三角形，
∴∠BA0=60°，
∴∠PAB=90°-∠BAO=90°-60°=30°．
故选B．
解：连接OA，则有OA⊥PA，由于PB：BC=1：2，
∴设BC=2x，
则PB=OB=OA=x，PC=3x，
由切割线定理知，PA2=PB•PC=3x2，
∴PA=
| 3 |
tan∠P=OA：PA=1：
| 3 |
∴∠P=30°，
∴∠AOB=90°-∠P=90°-30°=60°，
∴△AOB是等边三角形，
∴∠BA0=60°，
∴∠PAB=90°-∠BAO=90°-60°=30°．
故选B．
点评：本题利用了切割线定理，切线的性质，直角三角形的性质求解．
练习册系列答案
相关题目
