Question

如图，一条直线与反比例函数y=  的图象交于A(,2)，B(2,n)两点，与轴交于D点， AC⊥轴，垂足为C．

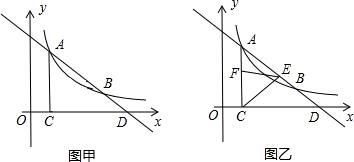
(1)如图甲，反比例函数的解析式为：______________；点D坐标为___________；
(2)如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，请求出F点的坐标．

Answer 1

（1）① y =  …………1分        ②D (,0) ………1分
（2）①证明略.…2分
②F₁(,2)；F₂(,1)；F₃(,4－2)………3分(共7分)解析:
（1）因为反比例函数图像过点A(,2)，所以，所以反比例函数解析式为
y = ，令，则，所以，B（2，），设直线解析式为，
把A、B两点坐标代入，可得，所以直线解析式为
当时，，故D点坐标为(,0)
①证明：∵A（,2），D（，0），AC⊥x轴
∴C（，0）
∴AC=CD=2，
即∠ADC=∠CAD=45°，
∵∠AEC=∠ECD+∠ADC=∠ECD+45°，
∠AEC=∠AEF+∠FEC=∠AEF+45°，
∴∠ECD=∠AEF，
△CDE和△EAF的两角对应相等，
∴△CDE∽△EAF．
②当CE=FE时，由△CDE≌△EAF可得AE=CD=2，∴F₁(,2)
当CE=CF时，由∠FEC=45°知∠ACE=90°，此时E与D重合，∴F与A重合∴F₂(,1)
当CF=EF时，由∠FEC=45°知∠CFE=90°，显然F为AC中点∴F₃(,4－2)
当△ECF为等腰三角形时，点F的坐标为F₁(,2)；F₂(,1)；F₃(,4－2)