题目内容
 如图,P、Q分别是△ABC边上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若PB=PQ,PR=PS.则下列结论:①AS=AR;②△BRP≌△QSP;③AQ+AB=2AR.其中正确的有
如图,P、Q分别是△ABC边上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若PB=PQ,PR=PS.则下列结论:①AS=AR;②△BRP≌△QSP;③AQ+AB=2AR.其中正确的有
- A.0个
- B.1个
- C.2个
- D.3个
D
分析:根据已知条件PR=PS可知AP为∠BAC的角平分线,利用HL易证△APR≌△APS,再利用全等三角形的性质可得AR=AS,同理利用HL易证△BPR≌△QPS,可知BR=SQ,利用等量代换可证AQ+AB=2AR.
解答:(1)∵PR⊥AB,PS⊥AC,垂足分别为R、S,若PR=PS.
∴AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∴△APR≌△APS,
∴AR=AS.
(2)∵PB=PQ,PR=PS.
∴△BPR≌△QPS;
(3)∵△BPR≌△QPS,
∴BR=SQ,
∴AQ+AB=(AS+SQ)+(AB-BR)=2AR.
即①②③都正确.
故选D.
点评:本题考查了全等三角形的判定和性质;做题时利用了平行线的判定、等边对等角、三角形外角的性质,要熟练掌握这些知识并能灵活应用.
分析:根据已知条件PR=PS可知AP为∠BAC的角平分线,利用HL易证△APR≌△APS,再利用全等三角形的性质可得AR=AS,同理利用HL易证△BPR≌△QPS,可知BR=SQ,利用等量代换可证AQ+AB=2AR.
解答:(1)∵PR⊥AB,PS⊥AC,垂足分别为R、S,若PR=PS.
∴AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∴△APR≌△APS,
∴AR=AS.
(2)∵PB=PQ,PR=PS.
∴△BPR≌△QPS;
(3)∵△BPR≌△QPS,
∴BR=SQ,
∴AQ+AB=(AS+SQ)+(AB-BR)=2AR.
即①②③都正确.
故选D.
点评:本题考查了全等三角形的判定和性质;做题时利用了平行线的判定、等边对等角、三角形外角的性质,要熟练掌握这些知识并能灵活应用.

练习册系列答案
相关题目

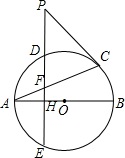 如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC.
如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC. 如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( )
如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( ) 已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF
已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF 桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.
桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.