题目内容
【题目】使得函数值为零的自变量的值称为函数的零点。例如,对于函数![]() ,令
,令![]() =0,可得
=0,可得![]() =1,我们就说1是函数
=1,我们就说1是函数![]() 的零点。 己知函数
的零点。 己知函数![]() (
(![]() 为常数)。
为常数)。
(1)当![]() =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论![]() 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,此时函数图象与
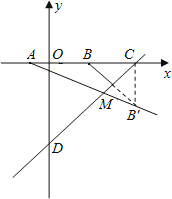
,此时函数图象与![]() 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线![]() 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
【答案】(1)![]() 和
和![]() ;(2)证明见解析;(3)AM的解析式为
;(2)证明见解析;(3)AM的解析式为![]()
【解析】
试题分析:(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式.
试题解析:(1)当![]() =0时,该函数为
=0时,该函数为![]() ,令
,令![]() =0,可得
=0,可得![]() ,
,
∴当![]() =0时,求该函数的零点为
=0时,求该函数的零点为![]() 和
和![]() 。
。
(2)令![]() =0,得△=
=0,得△=![]() ,
,
∴无论![]() 取何值,方程
取何值,方程![]() 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论![]() 取何值,该函数总有两个零点
取何值,该函数总有两个零点
(3)依题意有![]() ,
,![]()
由![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴函数的解析式为![]() 令
令![]() =0,解得
=0,解得![]() 。
。
∵点A在点B左侧,∴A(![]() ),B(4,0)。
),B(4,0)。
作点B关于直线![]() 的对称点B’,连结AB’,则AB’与直线
的对称点B’,连结AB’,则AB’与直线![]() 的交点就是满足条件的M点。易求得直线
的交点就是满足条件的M点。易求得直线![]() 与
与![]() 轴、
轴、![]() 轴的交点分别为C(10,0),D(0,10)。
轴的交点分别为C(10,0),D(0,10)。
连结CB’,则∠BCD=45°,∴BC=CB’=6,∠B’CD=∠BCD=45°。
∴∠BCB’=90°,即B’(![]() )。设直线AB’的解析式为
)。设直线AB’的解析式为![]() ,则
,则
![]() ,解得
,解得![]() ∴直线AB’的解析式为
∴直线AB’的解析式为![]() ,
,
即AM的解析式为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目