题目内容
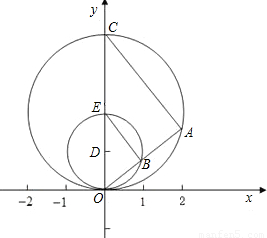
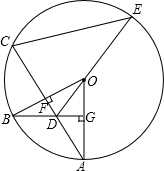 已知:G是⊙O的半径OA的中点,OA=
已知:G是⊙O的半径OA的中点,OA=| 3 |
①∠CEO=45°;②∠C=75°;③CD=2;④CE=
| 6 |
其中一定成立的是( )
| A、①②③④ | B、①②④ |
| C、①③④ | D、②③④ |
分析:①据30°角所对的直角边等于斜边的一半,可得∠OBG=30°,∠BOG=60°;可求得∠OAF=30°,连接OC,证明OC⊥OD,可得△OCE为等腰直角三角形,可得∠CEO=45°;
②∠C=∠ECO+∠OCD,说明∠OCF=30°即可得出∠C=75°;
③利用直角△COD的余弦函数,由∠OCD=30°,可求出CD=2;
④利用直角三角形的勾股定理,在△CEO中,可求得CE=
.
②∠C=∠ECO+∠OCD,说明∠OCF=30°即可得出∠C=75°;
③利用直角△COD的余弦函数,由∠OCD=30°,可求出CD=2;
④利用直角三角形的勾股定理,在△CEO中,可求得CE=
| 6 |
解答: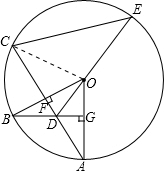 解:∵G是⊙O的半径OA的中点,OA=
解:∵G是⊙O的半径OA的中点,OA=
,
∴OG=
,
∵OB=OC=OE=OA=
,
∴OG=
OB,
∴∠OBG=30°,∠BOG=60°,
∴∠A=30°,
∵DG=DG,∠DGO=∠DGA=90°,OG=GA,
∴△DGO≌△DGA(SAS),
∴∠DOG=30°;
同理可证得∠DOF=30°,
∴∠ODF=60°.
又∵同理可证△COF≌△AOF,
∴∠OCF=30°.
∴∠OCF+∠ODF=90°,
∴∠DOC=90°,
∴OC⊥OD,
又∵OC=OE,
∴∠OCE=∠CEO=45°,故①结论成立;
∴∠C=∠OCF+∠OCE=30°+45°=75°,故②结论成立;
∵在直角△COD中,
=
,
∵OC=
,
∴CD=2,故③结论成立;
∵在直角△COE中,CE=
=
=
,∴④结论成立;
综上所述,故选A.
 解:∵G是⊙O的半径OA的中点,OA=
解:∵G是⊙O的半径OA的中点,OA=| 3 |
∴OG=
| ||
| 2 |
∵OB=OC=OE=OA=
| 3 |
∴OG=
| 1 |
| 2 |
∴∠OBG=30°,∠BOG=60°,
∴∠A=30°,
∵DG=DG,∠DGO=∠DGA=90°,OG=GA,
∴△DGO≌△DGA(SAS),
∴∠DOG=30°;
同理可证得∠DOF=30°,
∴∠ODF=60°.
又∵同理可证△COF≌△AOF,
∴∠OCF=30°.
∴∠OCF+∠ODF=90°,
∴∠DOC=90°,
∴OC⊥OD,
又∵OC=OE,
∴∠OCE=∠CEO=45°,故①结论成立;
∴∠C=∠OCF+∠OCE=30°+45°=75°,故②结论成立;
∵在直角△COD中,
| OC |
| CD |
| ||
| 2 |
∵OC=
| 3 |
∴CD=2,故③结论成立;
∵在直角△COE中,CE=
| OC2+OE2 |
(
|
| 6 |
综上所述,故选A.
点评:本题为综合考查题目,此类问题的解法是据已知条件,分别对每一个结论进行推理论证,最后得出结论来进行判断.

练习册系列答案
相关题目
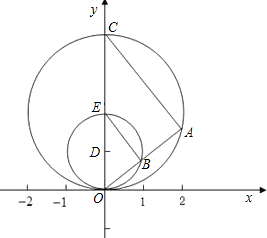 角形?若存在,求出点P的坐标;若不存在,说明其理由.
角形?若存在,求出点P的坐标;若不存在,说明其理由.