题目内容
（2012•中山一模）如图，在△ABC中，∠A=70°，AB=AC，CD平分∠ACB．求∠ADC的度数．分析：由AB=AC，且顶角∠A的度数，利用等边对等角得到两底角相等，且利用内角和定理求出底角的度数，再由CD为底角的平分线，求出∠DCB的度数，由∠ADC为三角形BCD的外角，利用外角性质即可求出∠ADC的度数．
解答：解：∵在△ABC中，∠A=70°，AB=AC，
∴∠B=∠ACB=
=55°，
又∵CD平分∠ACB，
∴∠DCB=∠ACD=27.5°，
∵∠ADC为△BCD的外角，
∴∠ADC=∠B+∠DCB=82.5°．
∴∠B=∠ACB=
| 180°-70° |
| 2 |
又∵CD平分∠ACB，
∴∠DCB=∠ACD=27.5°，
∵∠ADC为△BCD的外角，
∴∠ADC=∠B+∠DCB=82.5°．
点评：此题考查了等腰三角形的性质，三角形的外角性质，利用了方程的思想，其中等腰三角形的性质即为等边对等角．
练习册系列答案
相关题目
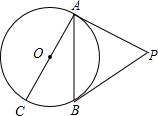（2012•中山一模）如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC=20°，求∠P的度数为（ ）
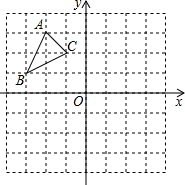（2012•中山一模）如图，△ABC中，A（-2，3），B（-3，1），C（-1，2）．