题目内容
(满分14分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为点F.

1.(1)求证:DF是⊙O的切线;
2.(2)若弧AE=弧DE,DF=2,求弧AD的长.
1.(1)证明:连结OD
∵AB=AC,∴∠C=∠B.………………………………………………2分
∵OD=OB,∴∠B=∠1.
∴∠C=∠1. ………………………………………………………3分
∴OD∥AC,∴∠2=∠FDO. ………………………………………4分
∵DF⊥AC,∴∠2=90°,∴∠FDO=90°,
即FD⊥OD且D点在⊙O 上---------------------------------5分
∴FD是圆O的切线.……………………………………6分
2.(2)∵AB是⊙O的直径,∴∠ADB=90°.…………7分
∵AC=AB,∴∠3=∠4………………………………8分
∴![]() ,∵
,∵![]() ,∴
,∴![]() ……………9分
……………9分
∴∠B=2∠4,∴∠B=60°,∠5=120°,
∴△ABC是等边三角形, ∠C=60°.………………………11分
在Rt△CFD中,sinC=![]() ,CD=
,CD= ,
,
∴DB= ,AB=BC=
,AB=BC=![]() ∴AO=
∴AO= .……………………13分
.……………………13分
∴![]() .………………………………………14分
.………………………………………14分

解析:略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由. 
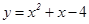 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线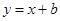 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.  ),其中
),其中 .
. 的值;(4分)
的值;(4分)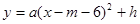 经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求
经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求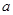 、
、 、
、