题目内容
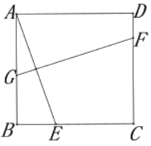
【题目】如图,在边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:

(1)画线段![]() ,且使
,且使![]() ,连接
,连接![]() ;
;
(2)线段![]() 的长为________,
的长为________,![]() 的长为________,
的长为________,![]() 的长为________;
的长为________;
(3)![]() 是________三角形,四边形
是________三角形,四边形![]() 的面积是________;
的面积是________;
(4)若点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】(1)见解析;(2)![]() ,
,![]() ,5;(3)直角,10;(4)
,5;(3)直角,10;(4)![]()
【解析】
(1)根据题意,画出AD∥BC且使AD=BC,连接CD;
(2)在网格中利用直角三角形,先求AC ![]() 的值,再求出AC的长,CD的长,AD的长;
的值,再求出AC的长,CD的长,AD的长;
(3)利用勾股定理的逆定理判断直角三角形,再求出四边形ABCD的面积;
(4)把问题转化到Rt△ACB中,利用直角三角形斜边上的中线可知BE=AE=EC,根据等腰三角形性质即可解题.
(1)如图所示:AD、CD为所求作
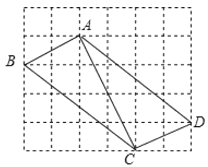
(2)根据勾股定理得:![]()
故答案为:![]() ;
;![]() ;5
;5
(3)∵![]() ,
,![]()
∴![]()
∴![]() 是直角三角形,∠ACD=90°
是直角三角形,∠ACD=90°
∴四边形![]() 的面积是:
的面积是:![]()
故答案为:直角;10
(4)∵![]() ,
,![]()
∴四边形ABCD是平行四边形
∴AB//CD
∴∠BAC=∠ACD=90°
在Rt△ACD中,![]() 为
为![]() 的中点
的中点
∴AE=BE=CE, ∠ABC+∠ACB=90°
∴∠ACB=∠EAC=27°
∴∠ABC =63°
故答案为:![]()

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目