题目内容
阅读材料：设一元二次方程ax2+bx+c=0的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1x2=
．
根据该材料解题：
关于x的方程kx2+(k+2)x+
=0有两个不相等的实数根．
①求k的取值范围．
②是否存在实数k，使方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
| b |
| a |
| c |
| a |
根据该材料解题：
关于x的方程kx2+(k+2)x+
| k |
| 4 |
①求k的取值范围．
②是否存在实数k，使方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
分析：（1）根据根的判别式得到k≠0，且△=（k+2）2-4k•
＞0，然后求出它们的公共部分即可得到k的取值范围是k＞-1，且k≠0；
（2）设方程kx2+（k+2）x+
=0的两根分别为x1、x2，由根与系数关系有：x1+x2=-
，x1•x2=
，当
+
=0，得到k=-2，不满足（1）中的条件，所以不存在符合条件的k的值．
| k |
| 4 |
（2）设方程kx2+（k+2）x+
| k |
| 4 |
| k+2 |
| k |
| 1 |
| 4 |
| 1 |
| x1 |
| 1 |
| x2 |
解答：解：（1）∵△=（k+2）2-4k•
＞0，
∴k＞-1，
又∵k≠0，
∴k的取值范围是k＞-1，且k≠0；
（2）不存在符合条件的实数k．理由如下：
设方程kx2+（k+2）x+
=0的两根分别为x1、x2，由根与系数关系有：x1+x2=-
，x1•x2=
，
而
+
=0，
∴-
=0，
∴k=-2，
由（1）知，k=-2时，△＜0，原方程无实解，
∴不存在符合条件的k的值．
| k |
| 4 |
∴k＞-1，
又∵k≠0，
∴k的取值范围是k＞-1，且k≠0；
（2）不存在符合条件的实数k．理由如下：
设方程kx2+（k+2）x+
| k |
| 4 |
| k+2 |
| k |
| 1 |
| 4 |
而
| 1 |
| x1 |
| 1 |
| x2 |
∴-
| k+2 |
| k |
∴k=-2，
由（1）知，k=-2时，△＜0，原方程无实解，
∴不存在符合条件的k的值．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程的两根为x1，x2，则x1+x2=-
，x1•x2=
．也考查了一元二次方程的根的判别式．
| b |
| a |
| c |
| a |
练习册系列答案
阅读快车系列答案
相关题目
20、阅读材料，解答问题．
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
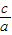根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，当0＜x1＜1，2＜x2＜3时，试判断y1与y2的大小关系．
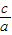，x1•x2=．根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+的值．（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 1 | 2 | 3 | … | |
| y | … | 5 | 2 | 1 | 2 | … |