题目内容
如图,A、B的坐标分别为(8,4),(0,4).点C从原点O出发以每秒1单位的速度沿着x轴的正方向运动,设运动时间为t(0<t<5).点D在x轴上,坐标为(t+3,0),过点D作x轴的垂线交AB于E点,交OA于G点,连接CE交OA于点F.(1)填空:CD=______,CE=______,AE=______ (用含t的代数式表示);
(2)当△EFG的面积为
 时,点G恰好在函数
时,点G恰好在函数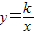 第一象限的图象上.试求出函数
第一象限的图象上.试求出函数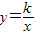 的解析式;
的解析式;(3)设点Q的坐标为(0,2t),点P在(2)中的函数
 的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.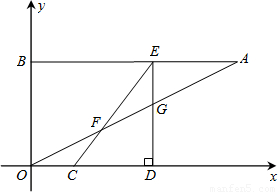
【答案】分析:(1)由OC=t,OD=t+3,即可求出CD的长;先由矩形的性质得出DE=4,然后在直角△CDE中,运用勾股定理即可求出CE的长;先由矩形的性质得出BE=t+3,再由AB=8即可求出AE的长;
(2)过点F作FH⊥DE于H,则△EFG的面积= EG•FH.先运用待定系数法求出直线OA的解析式,再将G点的横坐标(与D点的横坐标相等)代入,得到G点的纵坐标,求出EG的长;先由AE∥OC,得出△AEF∽△OCF,根据相似三角形对应边成比例列出等式AE:OC=EF:CF,得出EF=5-t,再由正弦函数的定义得出FH=EF•sin∠CED=
EG•FH.先运用待定系数法求出直线OA的解析式,再将G点的横坐标(与D点的横坐标相等)代入,得到G点的纵坐标,求出EG的长;先由AE∥OC,得出△AEF∽△OCF,根据相似三角形对应边成比例列出等式AE:OC=EF:CF,得出EF=5-t,再由正弦函数的定义得出FH=EF•sin∠CED= ,然后根据△EFG的面积为
,然后根据△EFG的面积为 列出关于t的方程,解方程求出t的值,得到G点的坐标为(4,2),则运用待定系数法即可求出过G点的反比例函数的解析式;
列出关于t的方程,解方程求出t的值,得到G点的坐标为(4,2),则运用待定系数法即可求出过G点的反比例函数的解析式;
(3)当以A、C、Q、P为顶点的四边形是平行四边形时,首先根据这四个点的位置及0<t<5,判断平行四边形可能是?APCQ或?APQC,再由平行四边形的对角线互相平分的性质得出两对角线的中点重合.设P(x, ),根据中点坐标公式列出关于x、t的方程组,解方程组即可.
),根据中点坐标公式列出关于x、t的方程组,解方程组即可.
解答:解:(1)∵由题意,可知OC=t,OD=t+3,
∴CD=OD-OC=t+3-t=3;
在直角△CDE中,∵∠CDE=90°,CD=3,DE=OB=4,
∴CE= =5;
=5;
∵AB=8,BE=OD=t+3,
∴AE=AB-BE=8-(t+3)=5-t.
故答案为3,5,5-t;
 (2)如图,过点F作FH⊥DE于H,则△EFG的面积=
(2)如图,过点F作FH⊥DE于H,则△EFG的面积= EG•FH.
EG•FH.
∵O(0,0),A(8,4),
∴直线OA的解析式为y= x,
x,
当x=t+3时,y= ,∴G(t+3,
,∴G(t+3, ),
),
∴EG=DE-DG=4- =
= .
.
∵AE∥OC,
∴△AEF∽△OCF,
∴AE:OC=EF:CF,即(5-t):t=EF:(5-EF),
解得EF=5-t,
∴FH=EF•sin∠CED=(5-t)× =
= ,
,
∴△EFG的面积= EG•FH=
EG•FH= ×
× ×
× =
= ,
,
∵△EFG的面积为 ,
,
∴ =
= ,
,
解得t=1或9,
∵0<t<5,
∴t=1,
∴G(4,2).
∵点G在函数 第一象限的图象上,
第一象限的图象上,
∴k=4×2=8.
故所求函数的解析式为y= ;
;
(3)当点Q的坐标为(0,2t),点P在(2)中的函数 的图象上时,存在以A、C、Q、P为顶点的平行四边形,理由如下:
的图象上时,存在以A、C、Q、P为顶点的平行四边形,理由如下:
分两种情况:设P(x, ).
).
①当四边形APCQ是平行四边形时,则AC与PQ互相平分,即AC的中点与PQ的中点重合.
∵A(8,4),C(t,0),Q(0,2t),
∴ ,
,
解得 ,
, (舍去),
(舍去),
∴C( -3,0),P(5+
-3,0),P(5+ ,10-2
,10-2 ).
).
②当四边形APQC是平行四边形时,则AQ与CP互相平分,即AQ的中点与CP的中点重合.
∵A(8,4),C(t,0),Q(0,2t),
∴ ,
,
解得 (舍去),
(舍去), (舍去).
(舍去).
综上可知,所求C点的坐标为( -3,0),P点的坐标为(5+
-3,0),P点的坐标为(5+ ,10-2
,10-2 ).
).
点评:本题考查了反比例函数的综合题,其中涉及到的知识点有矩形的性质、函数解析式的求法、三角形的面积、平行四边形的性质等,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,属于中档题.
(2)过点F作FH⊥DE于H,则△EFG的面积=
 EG•FH.先运用待定系数法求出直线OA的解析式,再将G点的横坐标(与D点的横坐标相等)代入,得到G点的纵坐标,求出EG的长;先由AE∥OC,得出△AEF∽△OCF,根据相似三角形对应边成比例列出等式AE:OC=EF:CF,得出EF=5-t,再由正弦函数的定义得出FH=EF•sin∠CED=
EG•FH.先运用待定系数法求出直线OA的解析式,再将G点的横坐标(与D点的横坐标相等)代入,得到G点的纵坐标,求出EG的长;先由AE∥OC,得出△AEF∽△OCF,根据相似三角形对应边成比例列出等式AE:OC=EF:CF,得出EF=5-t,再由正弦函数的定义得出FH=EF•sin∠CED= ,然后根据△EFG的面积为
,然后根据△EFG的面积为 列出关于t的方程,解方程求出t的值,得到G点的坐标为(4,2),则运用待定系数法即可求出过G点的反比例函数的解析式;
列出关于t的方程,解方程求出t的值,得到G点的坐标为(4,2),则运用待定系数法即可求出过G点的反比例函数的解析式;(3)当以A、C、Q、P为顶点的四边形是平行四边形时,首先根据这四个点的位置及0<t<5,判断平行四边形可能是?APCQ或?APQC,再由平行四边形的对角线互相平分的性质得出两对角线的中点重合.设P(x,
 ),根据中点坐标公式列出关于x、t的方程组,解方程组即可.
),根据中点坐标公式列出关于x、t的方程组,解方程组即可.解答:解:(1)∵由题意,可知OC=t,OD=t+3,
∴CD=OD-OC=t+3-t=3;
在直角△CDE中,∵∠CDE=90°,CD=3,DE=OB=4,
∴CE=
 =5;
=5;∵AB=8,BE=OD=t+3,
∴AE=AB-BE=8-(t+3)=5-t.
故答案为3,5,5-t;
 (2)如图,过点F作FH⊥DE于H,则△EFG的面积=
(2)如图,过点F作FH⊥DE于H,则△EFG的面积= EG•FH.
EG•FH.∵O(0,0),A(8,4),
∴直线OA的解析式为y=
 x,
x,当x=t+3时,y=
 ,∴G(t+3,
,∴G(t+3, ),
),∴EG=DE-DG=4-
 =
= .
.∵AE∥OC,
∴△AEF∽△OCF,
∴AE:OC=EF:CF,即(5-t):t=EF:(5-EF),
解得EF=5-t,
∴FH=EF•sin∠CED=(5-t)×
 =
= ,
,∴△EFG的面积=
 EG•FH=
EG•FH= ×
× ×
× =
= ,
,∵△EFG的面积为
 ,
,∴
 =
= ,
,解得t=1或9,
∵0<t<5,
∴t=1,
∴G(4,2).
∵点G在函数
 第一象限的图象上,
第一象限的图象上,∴k=4×2=8.
故所求函数的解析式为y=
 ;
;(3)当点Q的坐标为(0,2t),点P在(2)中的函数
 的图象上时,存在以A、C、Q、P为顶点的平行四边形,理由如下:
的图象上时,存在以A、C、Q、P为顶点的平行四边形,理由如下:分两种情况:设P(x,
 ).
).①当四边形APCQ是平行四边形时,则AC与PQ互相平分,即AC的中点与PQ的中点重合.
∵A(8,4),C(t,0),Q(0,2t),
∴
 ,
,解得
 ,
, (舍去),
(舍去),∴C(
 -3,0),P(5+
-3,0),P(5+ ,10-2
,10-2 ).
).②当四边形APQC是平行四边形时,则AQ与CP互相平分,即AQ的中点与CP的中点重合.
∵A(8,4),C(t,0),Q(0,2t),
∴
 ,
,解得
 (舍去),
(舍去), (舍去).
(舍去).综上可知,所求C点的坐标为(
 -3,0),P点的坐标为(5+
-3,0),P点的坐标为(5+ ,10-2
,10-2 ).
).点评:本题考查了反比例函数的综合题,其中涉及到的知识点有矩形的性质、函数解析式的求法、三角形的面积、平行四边形的性质等,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
 如图,A、B两点的坐标分别是A(
如图,A、B两点的坐标分别是A(| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图:A,B两点的坐标分别是(2,
如图:A,B两点的坐标分别是(2, 如图,A、B两点的坐标分别是(-3,0),(0,4),M是y轴上一点,沿AM折叠,AB刚好落在x轴上AB′处,求直线AM的解析式.
如图,A、B两点的坐标分别是(-3,0),(0,4),M是y轴上一点,沿AM折叠,AB刚好落在x轴上AB′处,求直线AM的解析式.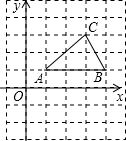 换得到△ABD.
换得到△ABD. 如图,A,B两点的坐标分别是
如图,A,B两点的坐标分别是