Question

【题目】（本小题满分9分）如图，在中，∠A=90°，AB=AC=4 cm，若O是BC的中点，动点M在AB上移动，动点N在AC上移动，且AN=BM ．

（1）证明：OM = ON；

（2）在点M，N运动的过程中，四边形AMON的面积是否发生变化，若发生变化，请说明理由；若不变，请你求出四边形AMON的面积．

Answer 1

【答案】见解析

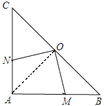
【解析】（1）连接OA（如图）.

∵在RtABC中，AB=AC，∴ABC是等腰直角三角形，

∴∠ABC=45°，即∠ABO=45°.（2分）

∵O是BC的中点，且ABC是等腰直角三角形，

∴AO⊥BC，

∴在AOB中，∠OAB=90°∠ABO=90°45°=45°，

∴∠OAB=∠ABO，

∴OA=OB，

∵O是BC的中点，且是等腰直角三角形，∠BAC=90°，

∴，

∴∠OAC=∠ABO=45°，即∠OAN=∠OBM，（3分）

∵在与中

，

∴，

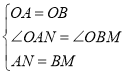∴ON=OM，即OM=ON.（5分）

（2）在动点M、N运动的过程中，四边形AMON的面积不变.（6分）

理由如下：

连接OA.

由第（1）小题的证明可知：，

∴△OAN的面积等于的面积，

∵四边形AMON的面积等于的面积与的面积之和，

∴四边形AMON的面积等于的面积与的面积之和，

∵的面积与的面积之和等于的面积，

∴四边形AMON的面积等于的面积，

∵O是BC的中点，且是等腰直角三角形，

∴△OAB的面积等于的面积的一半，（7分）

∵AB=AC=4 cm，

∴的面积为 (cm2)，

∴△OAB的面积为： (cm2)，

∴四边形AMON的面积为4 cm2.（9分）