Question

【题目】目前，我市正在积极创建文明城市，交通部门一再提醒司机：为了安全，请勿超速，并再进一步完善各类监测系统，如图，在某公路直线路段MN内限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据： =1.41， =1.73）

Answer 1

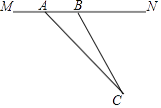
【答案】解：此车没有超速， 理由：如图，过点C作CH⊥MN于H，

在Rt△BCH中，∠CBN=60°，BC=200，
∴CH=BCsin60°=100 米，BH=BCcos60°=100米，
在Rt△AHC中，∠CAN=45°，
∴AH=CH=100 米，
∴AB=AH﹣BH=100 ﹣100≈73米，
∴车速为 =14.6m/s，
∵60km/h= m/s，而14.6＜ ，
∴此车没超速．
【解析】先构造出直角三角形，在Rt△BCH中，求出CH，BH，再在Rt△AHC中，求出AH，即可求出AB最后求出速度和行车速度比较即可．