题目内容
已知抛物线y=-
x2+mx过点(8,0),
(1)求m的值;
(2)如图a,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在x轴上,设矩形ABCD的周长为L,求L的最大值;
(3)如图b,抛物线的顶点为E,对称轴与直线y=-x+1交于点F.将直线EF向右平移n个单位后(n>0),交直线y=-x+1于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求n的值.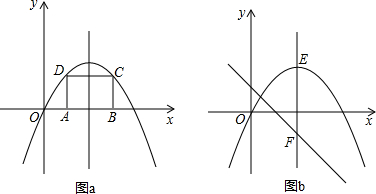
| 1 | 2 |
(1)求m的值;
(2)如图a,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在x轴上,设矩形ABCD的周长为L,求L的最大值;
(3)如图b,抛物线的顶点为E,对称轴与直线y=-x+1交于点F.将直线EF向右平移n个单位后(n>0),交直线y=-x+1于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求n的值.

分析:(1)根据抛物线y=-
x2+mx过点(8,0),直接代入求出m即可;
(2)利用配方法求出二次函数的顶点坐标,进而得出A点坐标,以及D点坐标,再利用二次函数的最值求出即可;
(3)根据①当四边形EFNM是平行四边形以及②当四边形EFMN是平行四边形分别求出即可.
| 1 |
| 2 |
(2)利用配方法求出二次函数的顶点坐标,进而得出A点坐标,以及D点坐标,再利用二次函数的最值求出即可;
(3)根据①当四边形EFNM是平行四边形以及②当四边形EFMN是平行四边形分别求出即可.
解答:解:(1)
∵抛物线y=-
x2+mx过点(8,0),
∴0=-
×64+8m,
∴m=4,
(2)抛物线y=-
x2+4x=-
(x-4)2+8,
设A点横坐标为m,则AB=8-2m,D(m,-
m2+4m),
∴矩形ABCD的周长=2(AD+AB)=2(8-2m-
m2+4m)=-(m-2)2+20,
∵a=-1<0,∴当m=2,矩形ABCD的周长的最大值为20,
(3)直线EF向右平移n个单位(n>0)使得E、F、M、N为顶点的四边形是平行四边形,
直线MN的解析式为x=4+n,直线MN与直线y=-x+1交于点M(4+n,-n-3),
又∵E(4,8),F(4,-3),
∴E通过向右平移11个单位得到F.
∵E、F、M、N为顶点的四边形是平行四边形,
∴四边形FEMN是平行四边形或四边形EFNM是平行四边形.
①当四边形EFNM是平行四边形,∴M向右平移11个单位得N,
∴N坐标为(4+n,-n-14),
又N在抛物线y=-
x2+4x上,
∴n2-2n-44=0,
解得n1=1+3
,n2=1-3
(不合题意,舍去)
②当四边形EFMN是平行四边形,∴M向右平移11个单位得N,
∴N坐标为(4+n,-n+8),
又N在抛物线y=-
x2+4x上,
∴n2-2n=0,
解得n1=2,n2=0(不合题意,舍去),
∴n的值为2,1+3
.
∵抛物线y=-
| 1 |
| 2 |
∴0=-
| 1 |
| 2 |
∴m=4,
(2)抛物线y=-
| 1 |
| 2 |
| 1 |
| 2 |
设A点横坐标为m,则AB=8-2m,D(m,-
| 1 |
| 2 |
∴矩形ABCD的周长=2(AD+AB)=2(8-2m-
| 1 |
| 2 |
∵a=-1<0,∴当m=2,矩形ABCD的周长的最大值为20,
(3)直线EF向右平移n个单位(n>0)使得E、F、M、N为顶点的四边形是平行四边形,
直线MN的解析式为x=4+n,直线MN与直线y=-x+1交于点M(4+n,-n-3),
又∵E(4,8),F(4,-3),
∴E通过向右平移11个单位得到F.
∵E、F、M、N为顶点的四边形是平行四边形,
∴四边形FEMN是平行四边形或四边形EFNM是平行四边形.
①当四边形EFNM是平行四边形,∴M向右平移11个单位得N,
∴N坐标为(4+n,-n-14),
又N在抛物线y=-
| 1 |
| 2 |
∴n2-2n-44=0,
解得n1=1+3
| 5 |
| 5 |
②当四边形EFMN是平行四边形,∴M向右平移11个单位得N,
∴N坐标为(4+n,-n+8),
又N在抛物线y=-
| 1 |
| 2 |
∴n2-2n=0,
解得n1=2,n2=0(不合题意,舍去),
∴n的值为2,1+3
| 5 |
点评:此题主要考查了二次函数的综合应用以及平行四边形的性质和点的坐标性质,利用分类讨论得出n的不同值是解题关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 已知抛物线y=-
已知抛物线y=-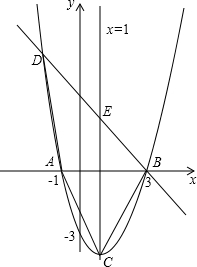 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3).