题目内容
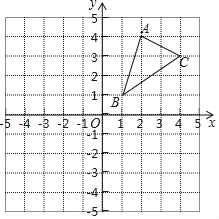
【题目】平面直角坐标系中，已知：A（2，3），B（4，4），C（5，1），在x轴上找一点D，使四边形ABCD的周长最小．
（1）在图中作出D点；（2）求出D点坐标．
【答案】(1)见解析;(2)D的坐标为（
，0）．
【解析】
（1）根据题意作C点关于Y轴的对称点C′点，并连接AC′与X的交点即可.
（2）根据题意得出C′的坐标为（5，﹣1），再求出直线AC′的解析式，即可得到D点的坐标.
解：（1）作点C关于x轴的对称点C′，连接AC′，则AC′与x轴的交点即为点D的位置，如图所示：
（2）∵点C坐标为（5，1），
∴C′的坐标为（5，﹣1）
∵点A坐标为（2，3），
设直线AC′的解析式为y＝kx＋b，
∴
，
解得
，
∴直线AC′的解析式为：y＝
x＋，
故点D的坐标为（，0）．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
