题目内容
已知抛物线y=ax2+bx+3,与x轴交于A(-3,0)、B(1,0),与y轴交于点C.
(1)求抛物线的解析式及顶点坐标;
(2)在平面直角坐标系中,是否存在点D,是以A、B、C、D为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标,若不存在,请说明理由;
(3)在抛物线的对称轴l上存在点Q,使△ACQ为直角三角形,请求出点Q的坐标.
解:(1)依题意,得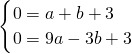 ,
,
解得,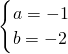 ,
,
抛物线的解析式为y=-x2-2x+3,
顶点坐标为(-1,4);
(2)如图,∵AB=4,OC=3,
∴CD1=CD2=AB=4,
D的坐标为D1(-4,3),D2(4,3),
∵D3E=OC=3,AE=OB,可得E点坐标为(-2,0),
∴D3(-2,-3);
(3)抛物线y=-x2-2x+3与y轴的交点C的坐标为(0,3),
设点Q的坐标为(-1,m),
①若∠QAC=90°,如图1,设抛物线的对称轴与x轴的交点
为E,则E(-1,0),则AE=2,EQ=-m,
由△AEQ∽△COA,得 ,
,
∴ ,
,
∴m=-2,
∴点Q的坐标为(-1,-2);
②若∠QCA=90°,如图2,作QF⊥y轴于点F,则QF=1,FC=m-3,
由△QFC∽△COA,得 ,
,
∴ ,
,
∴m=4,
∴点Q的坐标为(-1,4);
③若∠CQA=90°,如图3,设AC的中点为O1,则O1的坐标为
 ,作O1G⊥l于点G,则QG=
,作O1G⊥l于点G,则QG= ,O1G=
,O1G= ,
,
由勾股定理得, ,
,
∵ ,
,
∴ ,
,
解得, ,
,
∴点Q的坐标为 ,
, ;
;
综上所述,使△ACQ为直角三角形,点Q的坐标为
(-1,-2)、(-1,4)、 或
或 .
.
分析:(1)将A(-3,0)、B(1,0)分别代入y=ax2+bx+3,组成关于a、b的方程组,解方程组即可求出a、b的值,从而得到二次函数解析式;
(2)根据题意画出图形,根据平行四边形的性质及AB的长为4,OC=3,即可轻松得出点D的坐标;
(3)抛物线y=-x2-2x+3与y轴的交点C的坐标为(0,3),设点Q的坐标为(-1,m),然后分三种情况讨论①若∠QAC=90°,△AEQ∽△COA,利用相似三角形的性质解答;②若∠QCA=90°,由△QFC∽△COA,利用相似三角形的性质解答;③若∠CQA=90°,作O1G⊥l于点G,则QG= ,O1G=
,O1G= ,
,
由勾股定理得到关于m的方程,解方程求出m的值.
点评:本题考查了二次函数综合题,涉及求函数解析式、平行四边形的性质、相似三角形的判定与性质、勾股定理,要注意分类讨论的作用.
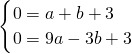 ,
,解得,
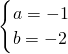 ,
,抛物线的解析式为y=-x2-2x+3,
顶点坐标为(-1,4);

(2)如图,∵AB=4,OC=3,
∴CD1=CD2=AB=4,
D的坐标为D1(-4,3),D2(4,3),
∵D3E=OC=3,AE=OB,可得E点坐标为(-2,0),
∴D3(-2,-3);
(3)抛物线y=-x2-2x+3与y轴的交点C的坐标为(0,3),
设点Q的坐标为(-1,m),
①若∠QAC=90°,如图1,设抛物线的对称轴与x轴的交点
为E,则E(-1,0),则AE=2,EQ=-m,

由△AEQ∽△COA,得
 ,
,∴
 ,
,∴m=-2,
∴点Q的坐标为(-1,-2);
②若∠QCA=90°,如图2,作QF⊥y轴于点F,则QF=1,FC=m-3,
由△QFC∽△COA,得
 ,
,∴
 ,
,∴m=4,
∴点Q的坐标为(-1,4);
③若∠CQA=90°,如图3,设AC的中点为O1,则O1的坐标为

 ,作O1G⊥l于点G,则QG=
,作O1G⊥l于点G,则QG= ,O1G=
,O1G= ,
,由勾股定理得,
 ,
,∵
 ,
,∴
 ,
,解得,
 ,
,∴点Q的坐标为
 ,
, ;
; 综上所述,使△ACQ为直角三角形,点Q的坐标为
(-1,-2)、(-1,4)、
 或
或 .
.分析:(1)将A(-3,0)、B(1,0)分别代入y=ax2+bx+3,组成关于a、b的方程组,解方程组即可求出a、b的值,从而得到二次函数解析式;
(2)根据题意画出图形,根据平行四边形的性质及AB的长为4,OC=3,即可轻松得出点D的坐标;
(3)抛物线y=-x2-2x+3与y轴的交点C的坐标为(0,3),设点Q的坐标为(-1,m),然后分三种情况讨论①若∠QAC=90°,△AEQ∽△COA,利用相似三角形的性质解答;②若∠QCA=90°,由△QFC∽△COA,利用相似三角形的性质解答;③若∠CQA=90°,作O1G⊥l于点G,则QG=
 ,O1G=
,O1G= ,
,由勾股定理得到关于m的方程,解方程求出m的值.
点评:本题考查了二次函数综合题,涉及求函数解析式、平行四边形的性质、相似三角形的判定与性质、勾股定理,要注意分类讨论的作用.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=