题目内容
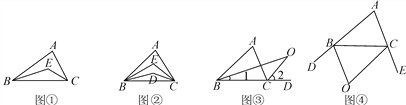
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么tan∠ADE的值为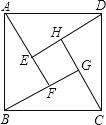
【答案】
【解析】解：设小正方形EFGH面积是a2 ， 则大正方形ABCD的面积是13a2 ， ∴小正方形EFGH边长是a，则大正方形ABCD的面积是 
a，
∵图中的四个直角三角形是全等的，
∴AE=DH，
设AE=DH=x，
在Rt△AED中，AD2=AE2+DE2 ，
即13a2=x2+（x+a）2
解得：x1=2a，x2=﹣3a（舍去），
∴AE=2a，DE=3a，
∴tan∠ADE= 
，故答案为： 
．
小正方形EFGH面积是a2 ， 则大正方形ABCD的面积是13a2 ， 则小正方形EFGH边长是a，则大正方形ABCD的面积是 a，设AE=DH=x，利用勾股定理求出x，最后利用熟记函数即可解答．此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边，进一步运用锐角三角函数的定义求解．
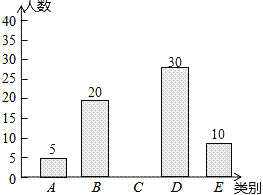
【题目】亚健康是时下社会热门话题，进行体育锻炼是远离亚健康的一种重要方式，为了解某校八年级学生每天进行体育锻炼的时间情况，随机抽样调查了100名初中学生，根据调查结果得到如图所示的统计图表．
类别 | 时间t（小时） | 人数 |
A | t≤0.5 | 5 |
B | 0.5＜t≤1 | 20 |
C | 1＜t≤1.5 | a |
D | 1.5＜t≤2 | 30 |
E | t＞2 | 10 |
请根据图表信息解答下列问题：
（1）a= ；
（2）补全条形统计图；
（3）小王说：“我每天的锻炼时间是调查所得数据的中位数”，问小王每天进行体育锻炼的时间在什么范围内？
（4）若把每天进行体育锻炼的时间在1小时以上定为锻炼达标，则被抽查学生的达标率是多少？
【题目】某校为了了解学生大课间活动的跳绳情况，随机抽取了50名学生每分钟跳绳的次数进行统计，把统计结果绘制成如表和直方图．
次数 | 70≤x＜90 | 90≤x＜110 | 110≤x＜130 | 130≤x＜150 | 150≤x＜170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息，回答下列问题：
（1）本次调查的样本容量是；
（2）本次调查中每分钟跳绳次数达到110次以上（含110次）的共有的共有人；
（3）根据上表的数据补全直方图；
（4）如果跳绳次数达到130次以上的3人中有2名女生和一名男生，学校从这3人中抽取2名学生进行经验交流，求恰好抽中一男一女的概率（要求用列表法或树状图写出分析过程）．
