题目内容
20.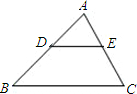 如图,已知:DE∥BC,若AD:AB=1:2,则S△ADE:S△ABC的值为1:4.
如图,已知:DE∥BC,若AD:AB=1:2,则S△ADE:S△ABC的值为1:4.
分析 根据两直线平行,可以得出△ADE∽△ABC,所以由相似三角形的性质得出S△ADE:S△ABC的值.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(AD:AB)2,
∵AD:AB=1:2,
∴S△ADE:S△ABC=1:4.
故答案为:1:4.
点评 本题考查了相似三角形的判定和性质,以及平行线的性质在三角形中的应用,两个相似三角形的边之比的平方等于面积之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.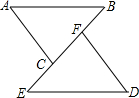 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
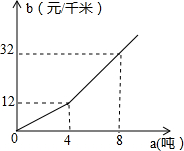 某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.
某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.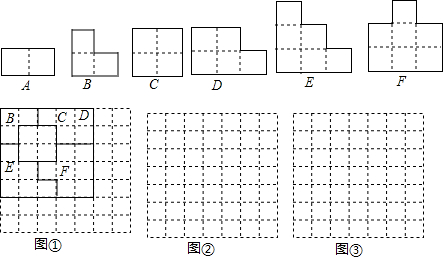
 如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.
如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.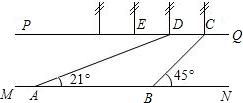 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).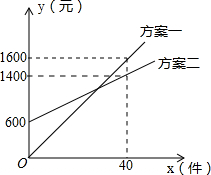 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题: