题目内容
(2013•台湾)若一元二次方程式a(x-b)2=7的两根为
±
,其中a、b为两数,则a+b之值为何?( )
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
分析:首先同时除以a得:(x-b)2=
,再两边直接开平方可得:x-b=±
,然后把-b移到右边,再根据方程的两根可得a、b的值,进而算出a+b的值.
| 7 |
| a |
|
解答:解:a(x-b)2=7,
两边同时除以a得:(x-b)2=
,
两边直接开平方可得:x-b=±
,
则x=±
+b,
∵两根为
±
,
∴a=4,b=
,
∴a+b=4
=
,
故选:B.
两边同时除以a得:(x-b)2=
| 7 |
| a |
两边直接开平方可得:x-b=±
|
则x=±
|
∵两根为
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
∴a=4,b=
| 1 |
| 2 |
∴a+b=4
| 1 |
| 2 |
| 9 |
| 2 |
故选:B.
点评:此题主要考查了直接开平方法解一元二次方程,关键是将方程右侧看做一个非负已知数,根据法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”来求解.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
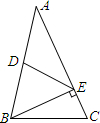 (2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )
(2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )