题目内容
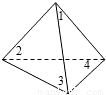
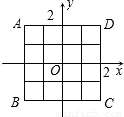
 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为
| 3 | 4 |
分析:(1)依题意得点P的横坐标有数字1,2,3,4四种选择,纵坐标也有数字1,2,3,4四种选择,故点P的坐标共有16种情况,有四种情况将落在正方形ABCD上,所以概率为
.
(2)要使点P落在正方形面上的概率为
,所以要将正方形移动使之符合.
| 1 |
| 4 |
(2)要使点P落在正方形面上的概率为
| 3 |
| 4 |
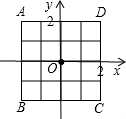
解答:解:(1)根据题意,点P的横坐标有数字1,2,3,4四种选择,点P的纵坐标也有数字1,2,3,4四种选择,
所以构成点P的坐标共有4×4=16种情况.
如下图所示:

其中点P的(1,1),(1,2),(2,1),(2,2)四种情况将落在正方形ABCD面上,
故所求的概率为
=
.
(2)因为要使点P落在正方形ABCD面上的概率为
=
>
,所以只能将正方形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12.
∴存在满足题设要求的平移方式:先将正方形ABCD上移2个单位,后右移1个单位(先右后上亦可);
或先将正方形ABCD上移1个单位,后右移2个单位(先右后上亦可).
所以构成点P的坐标共有4×4=16种情况.
如下图所示:

其中点P的(1,1),(1,2),(2,1),(2,2)四种情况将落在正方形ABCD面上,
故所求的概率为
| 4 |
| 16 |
| 1 |
| 4 |
(2)因为要使点P落在正方形ABCD面上的概率为
| 3 |
| 4 |
| 12 |
| 16 |
| 1 |
| 4 |
∴存在满足题设要求的平移方式:先将正方形ABCD上移2个单位,后右移1个单位(先右后上亦可);
或先将正方形ABCD上移1个单位,后右移2个单位(先右后上亦可).
点评:本题综合考查了平移的性质,几何概率的知识以及正方形的性质.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
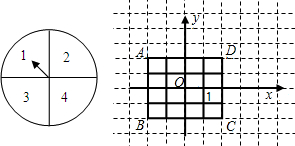 第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,则重新转动转盘.
第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,则重新转动转盘.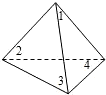
 (一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验: ?若存在,指出其中的一种平移方式;若不存在,请说明理由;
?若存在,指出其中的一种平移方式;若不存在,请说明理由;