题目内容
设O为△ABC内任意一点,AO,BO,CO分别交对边于A1,B1,C1,令 .求证:W≥12.
.求证:W≥12.
 证明:过A作AN⊥BC于N,过O作OM⊥BC于M,
证明:过A作AN⊥BC于N,过O作OM⊥BC于M,设△OBC、△OAB、△OAC的面积分别为Sa、Sc、Sb,
则AN∥OM,
∴
 =
= ,
,由面积公式得:
 =
= ,
,=
 ,
,=
 ,
,即:
 =
= ,
,同理:
 =
= ,
, =
= ,由基本不等式的性质的:
,由基本不等式的性质的: .
.再由平均值不等式得
 =
= .
.即W≥12,当且仅当O为三角形的重心时取等号.
∴W≥12.
分析:首先过A作AN⊥BC于N,过O作OM⊥BC于M,设△OBC、△OAB、△OAC的面积分别为Sa、Sc、Sb,根据三角形的面积公式求出
 、
、 、
、 的值,进一步计算出
的值,进一步计算出 •
• •
• 的值,再由平均值不等式进一步推出W≥3
的值,再由平均值不等式进一步推出W≥3 ,即可求出答案.
,即可求出答案.点评:本题主要考查了三角形的五心,三角形的面积公式,平均值不等式等知识点,正确利用三角形的面积公式和平均值不等式是解此题的关键.此题是一个拔高的题目,难度较大.

练习册系列答案
相关题目
 如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.
如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC. 【老题重现】
【老题重现】

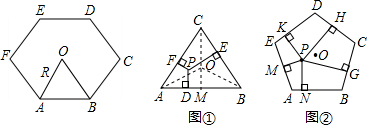 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系? 如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.
如图,设O为△ABC内一点,且∠AOB=∠BOC=∠COA=120°,P为任意一点(不是O).求证:PA+PB+PC>OA+OB+OC.