题目内容
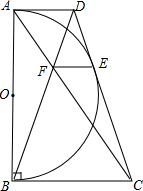 在直角梯形ABCD中,AD∥BC,以AB为直径作圆O恰好与CD相切于E,连AC、BD相交于F,连EF.
在直角梯形ABCD中,AD∥BC,以AB为直径作圆O恰好与CD相切于E,连AC、BD相交于F,连EF.
(1)求证:AB2=4AD•BC
(2)求证:EF∥BC
证明:(1)作DH⊥BC于H,如图,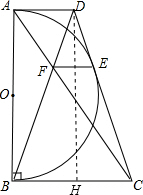
∵梯形ABCD为直角梯形,且AD∥BC,
∴四边形ABHD为矩形,
∴DH=AB,AD=BH,
∴CH=CB-AD,
∵以AB为直径作圆O恰好与CD相切于E,
∴DA、CB都是⊙O的切线,
∴DE=DA,CE=CB,
∴DC=DA+CB,
在Rt△DHC中,DH2=DC2-CH2,
∴AB2=(AD+BC)2-(BC-AD)2,
∴AB2=4AD•BC;
(2)∵AD∥BC,
∴△FDA∽△FBC,
∴ =
=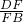 ,
,
而DE=AD,EC=BC,
∴ =
=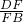 ,
,
∴EF∥BC.
分析:(1)作DH⊥BC于H,根据直角梯形的性质易得四边形ABHD为矩形,则DH=AB,AD=BH,于是CH=CB-AD,由以AB为直径作圆O恰好与CD相切于E,根据切线的判定定理得到DA、CB都是⊙O的切线,然后根据切线长定理得到DE=DA,CE=CB,即DC=DA+CB,在Rt△DHC中,利用勾股定理有DH2=DC2-CH2,即AB2=(AD+BC)2-(BC-AD)2,化简即可得到结论;
(2)由AD∥BC,根据三角形相似的判定方法易得△FDA∽△FBC,则 =
=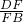 ,而DE=AD,EC=BC,于是有
,而DE=AD,EC=BC,于是有 =
=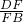 ,根据平行线分线段成比例定理的逆定理即可得到EF∥BC.
,根据平行线分线段成比例定理的逆定理即可得到EF∥BC.
点评:本题考查了圆的综合题:过半径的外端点与半径垂直的直线是圆的切线;从圆外一点引圆的两条切线,切线长相等;运用平行线分线段成比例定理的逆定理可解决线段平行的问题;运用相似三角形的判定与性质和勾股定理可解决线段之间的关系.

∵梯形ABCD为直角梯形,且AD∥BC,
∴四边形ABHD为矩形,
∴DH=AB,AD=BH,
∴CH=CB-AD,
∵以AB为直径作圆O恰好与CD相切于E,
∴DA、CB都是⊙O的切线,
∴DE=DA,CE=CB,
∴DC=DA+CB,
在Rt△DHC中,DH2=DC2-CH2,
∴AB2=(AD+BC)2-(BC-AD)2,
∴AB2=4AD•BC;
(2)∵AD∥BC,
∴△FDA∽△FBC,
∴
 =
=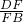 ,
,而DE=AD,EC=BC,
∴
 =
=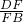 ,
,∴EF∥BC.
分析:(1)作DH⊥BC于H,根据直角梯形的性质易得四边形ABHD为矩形,则DH=AB,AD=BH,于是CH=CB-AD,由以AB为直径作圆O恰好与CD相切于E,根据切线的判定定理得到DA、CB都是⊙O的切线,然后根据切线长定理得到DE=DA,CE=CB,即DC=DA+CB,在Rt△DHC中,利用勾股定理有DH2=DC2-CH2,即AB2=(AD+BC)2-(BC-AD)2,化简即可得到结论;
(2)由AD∥BC,根据三角形相似的判定方法易得△FDA∽△FBC,则
 =
=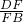 ,而DE=AD,EC=BC,于是有
,而DE=AD,EC=BC,于是有 =
=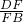 ,根据平行线分线段成比例定理的逆定理即可得到EF∥BC.
,根据平行线分线段成比例定理的逆定理即可得到EF∥BC.点评:本题考查了圆的综合题:过半径的外端点与半径垂直的直线是圆的切线;从圆外一点引圆的两条切线,切线长相等;运用平行线分线段成比例定理的逆定理可解决线段平行的问题;运用相似三角形的判定与性质和勾股定理可解决线段之间的关系.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
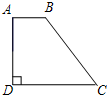 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )