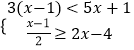题目内容
【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 . 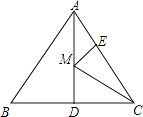
【答案】![]()
【解析】解:连接BE,与AD交于点M.则BE就是EM+CM的最小值. 取CE中点F,连接DF.
∵等边△ABC的边长为6,AE=2,
∴CE=AC﹣AE=6﹣2=4,
∴CF=EF=AE=2,
又∵AD是BC边上的中线,
∴DF是△BCE的中位线,
∴BE=2DF,BE∥DF,
又∵E为AF的中点,
∴M为AD的中点,
∴ME是△ADF的中位线,
∴DF=2ME,
∴BE=2DF=4ME,
∴BM=BE﹣ME=4ME﹣ME=3ME,
∴BE= ![]() BM.
BM.
在直角△BDM中,BD= ![]() BC=3,DM=
BC=3,DM= ![]() AD=
AD= ![]() ,
,
∴BM= ![]() =
= ![]() ,
,
∴BE= ![]() .
.
∵EM+CM=BE
∴EM+CM的最小值为 ![]() .
.
要求EM+CM的最小值,需考虑通过作辅助线转化EM,CM的值,从而找出其最小值求解.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目