题目内容
 如图,直角梯形ABCD中,AB∥CD,AB⊥BC,AB>CD,对角线AC、BD交于点O,OE⊥BC于E.
如图,直角梯形ABCD中,AB∥CD,AB⊥BC,AB>CD,对角线AC、BD交于点O,OE⊥BC于E.
(1)若BC=AB+CD,求证:CD=CE;
(2)取BC的中点F,若BC=10,OE+OF=5,求AB+CD的值.
(1)证明:∵CD∥OE∥AB,
∴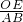 =
= ①,
①, =
= ②,
②,
∴①+②得: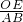 +
+ =1,
=1,
∴OE= =
= ,
,
代入①得 =
= ,
,
∴CD=CE.
(2)解:设EF=x,则BE=5+x,CE=5-x,
∴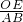 =
= =
= ,
,
∴AB= OE,
OE,
同理CD= OE,
OE,
∴AB+CD= OE,
OE,
∵OE2+EF2=OF2,
即OE2+x2=(5-OE)2,
∴OE= ,
,
∴AB+CD=10.
分析:(1)由CD∥OE∥AB得到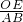 =
= ①,
①, =
= ②,然后①+②得
②,然后①+②得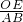 +
+ =1,然后变形得到OE=
=1,然后变形得到OE= =
= ,接着利用BC=AB+CD即可求解;
,接着利用BC=AB+CD即可求解;
(2)设EF=x,则BE=5+x,CE=5-x,代入①得到AB= OE,同理CD=
OE,同理CD= OE,接着得到AB+CD=
OE,接着得到AB+CD= OE,再利用勾股定理OE2+EF2=OF2得到OE=
OE,再利用勾股定理OE2+EF2=OF2得到OE= ,由此即可证明AB+CD=10.
,由此即可证明AB+CD=10.
点评:本题考查平行线分线段成比例定理,找准对应关系是解题的关键,然后避免错选其他答案.
∴
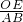 =
= ①,
①, =
= ②,
②,∴①+②得:
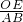 +
+ =1,
=1,∴OE=
 =
= ,
,代入①得
 =
= ,
,∴CD=CE.
(2)解:设EF=x,则BE=5+x,CE=5-x,
∴
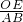 =
= =
= ,
,∴AB=
 OE,
OE,同理CD=
 OE,
OE,∴AB+CD=
 OE,
OE,∵OE2+EF2=OF2,
即OE2+x2=(5-OE)2,
∴OE=
 ,
,∴AB+CD=10.
分析:(1)由CD∥OE∥AB得到
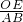 =
= ①,
①, =
= ②,然后①+②得
②,然后①+②得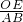 +
+ =1,然后变形得到OE=
=1,然后变形得到OE= =
= ,接着利用BC=AB+CD即可求解;
,接着利用BC=AB+CD即可求解; (2)设EF=x,则BE=5+x,CE=5-x,代入①得到AB=
 OE,同理CD=
OE,同理CD= OE,接着得到AB+CD=
OE,接着得到AB+CD= OE,再利用勾股定理OE2+EF2=OF2得到OE=
OE,再利用勾股定理OE2+EF2=OF2得到OE= ,由此即可证明AB+CD=10.
,由此即可证明AB+CD=10.点评:本题考查平行线分线段成比例定理,找准对应关系是解题的关键,然后避免错选其他答案.

练习册系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF. ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.