题目内容
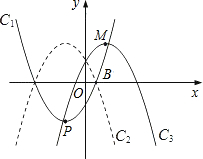
如图,已知抛物线C1: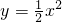 ,把它平移后得抛物线C2,使C2经过点A(0,8),且与抛物线C1交于点B(2,n).在x轴上有一点P,从原点O出发以每秒1个单位的速度沿x轴正半轴的方向移动,设点P移动的时间为t秒,过点P作x轴的垂线l,分别交抛物线C1、C2于E、D,当直线l经过点B前停止运动,以DE为边在直线l左侧画正方形DEFG.
,把它平移后得抛物线C2,使C2经过点A(0,8),且与抛物线C1交于点B(2,n).在x轴上有一点P,从原点O出发以每秒1个单位的速度沿x轴正半轴的方向移动,设点P移动的时间为t秒,过点P作x轴的垂线l,分别交抛物线C1、C2于E、D,当直线l经过点B前停止运动,以DE为边在直线l左侧画正方形DEFG.
(1)判断抛物线C2的顶点是否在x轴上,并说明理由;
(2)当t为何值时,正方形DEFG在y轴右侧的部分的面积S有最大值?最大值为多少?
(3)设M为正方形DEFG的对称中心.当t为何值时,△MOP为等腰三角形?
解:(1)抛物线C2的顶点在x轴上.理由如下:
∵点B(2,n)在抛物线C1上,
∴ ×22=n,
×22=n,
解得n=2,
∴点B的坐标为(2,2),
∵抛物线C2是抛物线C1平移得到,
∴设抛物线C2的解析式为y= x2+bx+c,
x2+bx+c,
又∵C2经过点A(0,8),
∴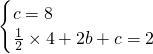 ,
,
解得 ,
,
∴抛物线C2的解析式为y= x2-4x+8=
x2-4x+8= (x-4)2,
(x-4)2,
∴抛物线C2的顶点在x轴上;
(2)时间为t时,点D、E的坐标分别为D(t, t2-4t+8),E(t,
t2-4t+8),E(t, t2),
t2),
∴DE= t2-4t+8-
t2-4t+8- t2=-4t+8,
t2=-4t+8,
∴S=OP•DE=t(-4t+8)=-4t2+8t=-4(t-1)2+4,
∵直线l经过点B前停止运动,
∴0<t<2,
∴当t=1时,正方形DEFG在y轴右侧的部分S有最大值,最大值为4;
(3)如图,可以判定当点M在y轴左侧时,△MOP不能为等腰三角形,
∴当点M在y轴右侧,且在OP的垂直平分线上时,△MOP为等腰三角形,
此时∵点M是正方形的中心,
∴ DE=
DE= OP,
OP,
即 (-4t+8)=
(-4t+8)= t,
t,
解得t= ,
,
∵ <2,
<2,
∴符合题意,
故当t= 时,△MOP为等腰三角形.
时,△MOP为等腰三角形.
分析:(1)把点B的坐标代入抛物线C1,进行计算求出n的值,从而得到点B的坐标,然后根据平移变换不改变二次函数图象的形状,设抛物线C2的解析式为y= x2+bx+c,然后利用待定系数法求解,再根据抛物线的顶点坐标进行判断;
x2+bx+c,然后利用待定系数法求解,再根据抛物线的顶点坐标进行判断;
(2)根据两抛物线的解析式表示出点D、E的坐标,然后求出DE的长度,然后根据矩形的面积公式列式整理,再根据二次函数的最值问题求解即可;
(3)根据正方形的性质结合抛物线的对称性可以判断,当正方形的中心在y轴右侧时,△MOP为等腰三角形,然后根据线段垂直平分线上的点到线段两端点的距离相等,可得点M到直线l的距离等于正方形边长的一半,然后列式求解即可.
点评:本题是对二次函数的综合考查,待定系数法求函数解析式,两点间的距离公式,正方形的性质,等腰三角形的性质,以及二次函数的最值问题,综合性较强,难度较大,需仔细分析并理解方可解决.
∵点B(2,n)在抛物线C1上,
∴
 ×22=n,
×22=n,解得n=2,
∴点B的坐标为(2,2),
∵抛物线C2是抛物线C1平移得到,
∴设抛物线C2的解析式为y=
 x2+bx+c,
x2+bx+c,又∵C2经过点A(0,8),
∴
 ,
,解得
 ,
,∴抛物线C2的解析式为y=
 x2-4x+8=
x2-4x+8= (x-4)2,
(x-4)2,∴抛物线C2的顶点在x轴上;
(2)时间为t时,点D、E的坐标分别为D(t,
 t2-4t+8),E(t,
t2-4t+8),E(t, t2),
t2),∴DE=
 t2-4t+8-
t2-4t+8- t2=-4t+8,
t2=-4t+8,∴S=OP•DE=t(-4t+8)=-4t2+8t=-4(t-1)2+4,

∵直线l经过点B前停止运动,
∴0<t<2,
∴当t=1时,正方形DEFG在y轴右侧的部分S有最大值,最大值为4;
(3)如图,可以判定当点M在y轴左侧时,△MOP不能为等腰三角形,
∴当点M在y轴右侧,且在OP的垂直平分线上时,△MOP为等腰三角形,
此时∵点M是正方形的中心,
∴
 DE=
DE= OP,
OP,即
 (-4t+8)=
(-4t+8)= t,
t,解得t=
 ,
,∵
 <2,
<2,∴符合题意,
故当t=
 时,△MOP为等腰三角形.
时,△MOP为等腰三角形.分析:(1)把点B的坐标代入抛物线C1,进行计算求出n的值,从而得到点B的坐标,然后根据平移变换不改变二次函数图象的形状,设抛物线C2的解析式为y=
 x2+bx+c,然后利用待定系数法求解,再根据抛物线的顶点坐标进行判断;
x2+bx+c,然后利用待定系数法求解,再根据抛物线的顶点坐标进行判断;(2)根据两抛物线的解析式表示出点D、E的坐标,然后求出DE的长度,然后根据矩形的面积公式列式整理,再根据二次函数的最值问题求解即可;
(3)根据正方形的性质结合抛物线的对称性可以判断,当正方形的中心在y轴右侧时,△MOP为等腰三角形,然后根据线段垂直平分线上的点到线段两端点的距离相等,可得点M到直线l的距离等于正方形边长的一半,然后列式求解即可.
点评:本题是对二次函数的综合考查,待定系数法求函数解析式,两点间的距离公式,正方形的性质,等腰三角形的性质,以及二次函数的最值问题,综合性较强,难度较大,需仔细分析并理解方可解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;