题目内容
在等腰梯形ABCD中,AD∥BC,AD<BC,AB=2,BC=4,∠B=60°,则该梯形的面积是
- A.2

- B.4-

- C.8
 -4
-4 - D.3

D
分析:过点A作AE∥CD,交BC于点E,此时等腰梯形被分成一个平行四边形和一个等边三角形,从而可求得AD及高的长再利用面积公式即可求得其面积.
解答: 解:过点A作AE∥CD,交BC于点E.由已知得出△ABE是等边三角形,
解:过点A作AE∥CD,交BC于点E.由已知得出△ABE是等边三角形,
∴BE=AB=2,
∴AD=CE=4-2=2,
△ABE的高为 ,
,
则该梯形的面积是 (2+4)×
(2+4)× =3
=3 .
.
故选D.
点评:此题考查等腰梯形的性质及梯形中常见的辅助线的作法.
分析:过点A作AE∥CD,交BC于点E,此时等腰梯形被分成一个平行四边形和一个等边三角形,从而可求得AD及高的长再利用面积公式即可求得其面积.
解答:
 解:过点A作AE∥CD,交BC于点E.由已知得出△ABE是等边三角形,
解:过点A作AE∥CD,交BC于点E.由已知得出△ABE是等边三角形,∴BE=AB=2,
∴AD=CE=4-2=2,
△ABE的高为
 ,
,则该梯形的面积是
 (2+4)×
(2+4)× =3
=3 .
.故选D.
点评:此题考查等腰梯形的性质及梯形中常见的辅助线的作法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.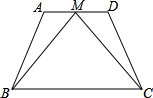 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.