题目内容
 将4个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则4个正方形重叠部分(图中阴影部分)的面积和是
将4个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,A3,A4分别是正方形的中心,则4个正方形重叠部分(图中阴影部分)的面积和是分析:由图形的特点可知,连接正方形的中心和其余两个顶点可证得含45°的两个三角形全等,进而求得每个阴影部分的面积都等于正方形面积的
,据此解题.
| 1 |
| 4 |
解答:解:连接正方形的中心和其余两个顶点可证得含45°的两个三角形全等,进而求得每个阴影部分的面积都等于正方形面积的
,
故图中三块阴影部分的面积和为一个正方形的面积的
,即
cm2.
故答案为
cm2.
| 1 |
| 4 |
故图中三块阴影部分的面积和为一个正方形的面积的
| 3 |
| 4 |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评:本题主要考查了正方形的特性及面积公式,解答本题的关键是发现每个阴影部分的面积都等于正方形面积的
.
| 1 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
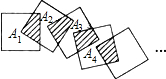 将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积和为( )
将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积和为( )A、
| ||
B、
| ||
C、
| ||
D、(
|
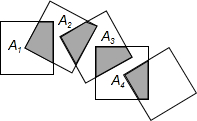 将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为( )cm2.
将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为( )cm2.A、
| ||
B、
| ||
C、
| ||
D、
|
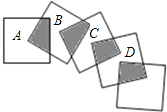 如图,所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是
如图,所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是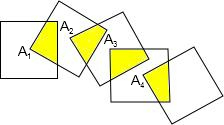
 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )