题目内容
在△ABC中,若a=1,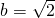 ,
, ,则△ABC的形状是
,则△ABC的形状是
- A.等腰三角形
- B.等腰三角形或钝角三角形
- C.等边三角形或钝角三角形
- D.等腰直角三角形或钝角三角形
D
分析:根据三角形的面积公式S= absinC,结合题干条件,求出sinC,进而求出∠C的度数,再判断三角形的形状.
absinC,结合题干条件,求出sinC,进而求出∠C的度数,再判断三角形的形状.
解答:根据三角形的面积公式S= absinC,又知a=1,b=
absinC,又知a=1,b= ,
, ,
,
即 =
=
 sinC,
sinC,
解得sinC= ,
,
又知0°<∠C<180°,
可得∠C=45°或135°,
当∠C=45°时,可求出另一边c=1,即△ABC的形状为等腰直角三角形,
当∠C=135°时,可知△ABC的形状为钝三角形,
故选D.
点评:本题主要考查勾股定理的知识点,解答本题的关键三角形的面积公式,此题难度一般.
分析:根据三角形的面积公式S=
 absinC,结合题干条件,求出sinC,进而求出∠C的度数,再判断三角形的形状.
absinC,结合题干条件,求出sinC,进而求出∠C的度数,再判断三角形的形状.解答:根据三角形的面积公式S=
 absinC,又知a=1,b=
absinC,又知a=1,b= ,
, ,
,即
 =
=
 sinC,
sinC,解得sinC=
 ,
,又知0°<∠C<180°,
可得∠C=45°或135°,
当∠C=45°时,可求出另一边c=1,即△ABC的形状为等腰直角三角形,
当∠C=135°时,可知△ABC的形状为钝三角形,
故选D.
点评:本题主要考查勾股定理的知识点,解答本题的关键三角形的面积公式,此题难度一般.

练习册系列答案
相关题目
 如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )
如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )