题目内容
M为矩形ABCD中AB边上的中点，且AB=2BC，那么∠CMB等于（ ）
| A、30° | B、45° |
| C、60° | D、75° |
考点：矩形的性质
专题：
分析：根据矩形的性质可知∠B=90°，因为AB=2BC，M为AB的中点，所以AM=BM，即BM=BC，所以△BMC是等腰直角三角形，问题得解．
解答：解：∵四边形ABCD是矩形，
∴∠B=90°，
∵M为AB的中点，
∴AM=BM=
AB，
∵AB=2BC，
∴BM=BC，
∴△BMC是等腰直角三角形，
∴∠CMB=45°，
故选B．
∴∠B=90°，∵M为AB的中点，
∴AM=BM=
| 1 |
| 2 |
∵AB=2BC，
∴BM=BC，
∴△BMC是等腰直角三角形，
∴∠CMB=45°，
故选B．
点评：本题考查了矩形的性质、等腰直角三角形的判定和性质以及线段中点的定义，题目比较简单．
练习册系列答案
相关题目
如图是一些国家的国旗，是轴对称图形的有（ ）
| A、甲乙丙丁戊 | B、甲乙丁戊 |
| C、甲乙丙戊 | D、甲乙戊 |
下列运算能运用平方差公式运算的是（ ）
| A、（a-b）（-a+b） |
| B、（x+y）（-x-y） |
| C、（1-xy）（-xy-1） |
| D、（a-b）（a-b） |
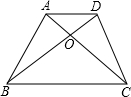如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O．若S△AOD：S△BOC=1：4，则S△AOD：S△ACD为（ ）| A、1：6 | B、1：5 |
| C、1：4 | D、1：3 |
下列语句中，属于命题的是（ ）
| A、直线AB和CD垂直吗？ |
| B、过线段AB的中点C画AB的垂线 |
| C、同旁内角互补，两直线平行 |
| D、连接A，B两点 |
已知△ABC∽△A′B′C′，且相似比为2．则（ ）
| A、∠A是∠A′的2倍 |
| B、∠A′是∠A的2倍 |
| C、AB是A′B′的2倍 |
| D、A′B′是AB的2倍 |
在反比例函数y=-
的图象上，坐标为整数的点的个数为（ ）
| 6 |
| x |
| A、4个 | B、6个 | C、8个 | D、10个 |