题目内容
如果|ab-2|+（b-1）2=0，试求：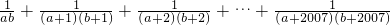
的值．
解：因为|ab-2|+（b-1）2=0，且|ab-2|≥0，（b-1）2≥0，
所以ab-2=0，b-1=0，
所以b=1，a=2，
所以原式=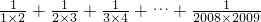
=1-
+-
+-
+…+
．
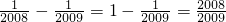分析：本题应先根据非负数的性质“两个非负数相加，和为0，这两个非负数的值都为0．”解出a、b的值，再把a、b的值代入代数式中，将分式化简求值．
点评：注意：将原有的分数拆成两个相减的分数，再对方程进行化简是此类分数的常见的解法．
所以ab-2=0，b-1=0，
所以b=1，a=2，
所以原式=
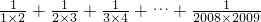
=1-
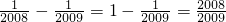+-+-+…+．分析：本题应先根据非负数的性质“两个非负数相加，和为0，这两个非负数的值都为0．”解出a、b的值，再把a、b的值代入代数式中，将分式化简求值．
点评：注意：将原有的分数拆成两个相减的分数，再对方程进行化简是此类分数的常见的解法．
练习册系列答案
相关题目
14、如图，在△ABC中，OB、OC分别是∠B和∠C的角平分线，过点O作EF∥BC，交AB、AC于点E、F，如果AB=10，AC=8，那么△AEF的周长为在△ABC中，∠C=90°，如果AB=2，BC=1，那么∠A的度数为（ ）
| A、30° | B、45° | C、60° | D、90° |
15、如图，根据SAS，如果AB=AC，
如图，在△ABC中，如果| AB |
| a |
| AC |
| b |
| a |
| b |
| A、BC | ||
B、
| ||
| C、CB | ||
D、
|