Question

【题目】如图，分别以Rt△ABC的三边为斜边向外作等腰直角三角形，若斜边AB=4，则图中阴影部分的面积为（ ）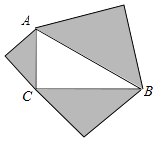
A.4
B.8
C.10
D.12

Answer 1

【答案】B
【解析】解：在Rt△AHC中，AC2=AH2+HC2 ， AH=HC， ∴AC2=2AH2 ，
∴HC=AH= ，
同理；CF=BF= ，BE=AE= ，
在Rt△ABC中，AB2=AC2+BC2 ， AB=4，
S阴影=S△AHC+S△BFC+S△AEB= HCAH+ CFBF+ AEBE，
= ×（ ）2+ ×（ ）2+ （ ）2= （AC2+BC2+AB2）
= （AB2+AB2）
= ×2AB2
= AB2
= ×42
=8．
故选B．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)．