题目内容
如图，在矩形ABCD中，AB=4cm，AD=2cm，动点M自点A出发沿A→B的方向，以每秒1cm的速度运动，同时动点N自点A出发沿A→D→C的方向以每秒2cm的速度运动，当点N到达点C时，两点同时停止运动，设运动时间为x（秒），△AMN的面积为y（cm2），则下列图象中能反映y与x之间的函数关系的是
D
在矩形ABCD中，AB=4cm，AD=2cm，
AD+DC=AB+AD=4+2=6cm，
∵点M以每秒1cm的速度运动，
∴4÷1=4秒，
∵点N以每秒2cm的速度运动，
∴6÷2=3秒，
∴点N先到达终点，运动时间为3秒，
①点N在AD上运动时，y=
AM?AN=x?2x=x2（0≤x≤1）；
②点N在DC上运动时，y=
AM?AD=x?2=x（1≤x≤3），
∴能反映y与x之间的函数关系的是D选项．
故选D．
AD+DC=AB+AD=4+2=6cm，
∵点M以每秒1cm的速度运动，
∴4÷1=4秒，
∵点N以每秒2cm的速度运动，
∴6÷2=3秒，
∴点N先到达终点，运动时间为3秒，
①点N在AD上运动时，y=
AM?AN=x?2x=x2（0≤x≤1）；②点N在DC上运动时，y=
AM?AD=
x?2=x（1≤x≤3），∴能反映y与x之间的函数关系的是D选项．
故选D．
练习册系列答案
相关题目
发生腹泻等肠道疾病，某市医药公司的甲、乙两仓库分别存有医治腹泻的药品80箱和70箱，现需要将库存的药品调往A地100箱和B地50箱。已知从甲、乙两仓库运送药品到两地的费用（元／箱）如下表所示：
箱，求总费用
（元）与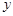
＝
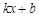（k≠0）与坐标轴分别交于A、B两点，OA、OB的长分别
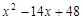＝0的两根（OA＞OB）．动点P从O点出发，沿路线O→B→A以每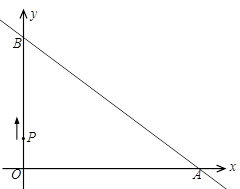
有意义，则x应满足（ ） 
（
）与
（
．