题目内容
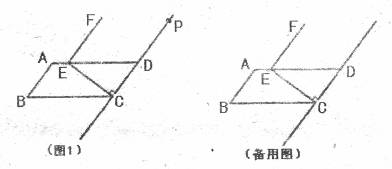
如图,在□ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF,点P为直线CD上一点(不与点C重合).
(1)在图1中画图探究:
当点P在CD延长线上时,连结EP并把EP绕点E逆时针旋转90°得到线段EQ.作直线QF交直线CD于H,求证:QF⊥CD.
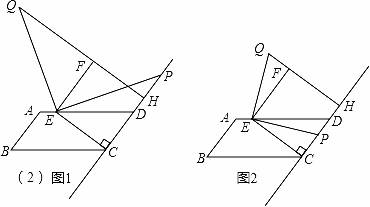
(2)探究:结合(1)中的画图步骤,分析线段QH、PH与CE之间是否存在一种特定的数量关系?请在下面的空格中写出你的结论;若存在,直接填写这个关系式.
①当点P在CD延长线上且位于H点右边时, _________ ;
②当点P在边CD上时, _________ .
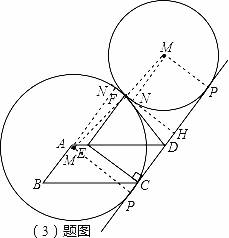
(3)若AD=2AB=6,AE=1,连接DF,过P、F两点作⊙M,使⊙M同时与直线CD、DF相切,求⊙M的半径是多少?
解:(1)由旋转的性质得,PE=QE,EF=ED,
∵∠QEF+∠FEP=∠PEQ=90°,
∠PEC+∠FEP=∠CEF=90°,
∴∠PEC=∠QEF,
在△PEC和△QEF中,
 ,
,
∴△PEC≌△QEF(SAS),
∴∠QFE=∠PCE=90°,
∵∠FEC+∠PCE=90°+90°=180°,
∴EF∥CD,
∴∠QHC=∠QFE=90°,
∴QF⊥CD;
(2)∵△PEC≌△QEF,
∴QF=PC,
∵∠PCE=∠CEF=∠QHC=90°,CE=EF,
∴四边形EFHC是正方形,
∴CH=FH=CE,
①如图1,当点P在CD延长线上且位于H点右边时,QH=QF+FH=PC+FH=PH+CH+FH=PH+2CE,
∴QH﹣PH=2CE;
②如图2,当点P在边CD上时,QH=QF+FH=PC+FH=CH﹣PH+FH=2CE﹣PH,
∴QF+PH=2CE;
(3)∵AD=6,AE=1,
∴DE=5,
在Rt△CDE中,CE=![]() =
=![]() =4,
=4,
∴DH=CH﹣CD=CE﹣CD=4﹣3=1,
在Rt△DFH中,FD=![]() =
=![]() =
=![]() ,
,
如图,过点M作MN⊥FH于N,
则四边形PMNH是矩形,
∵⊙M同时与直线CD、DF相切,
∴DP=FD=![]() ,
,
设⊙M的半径是r,
①点P在点D的右边时,在Rt△MNF中,FN=4﹣r,MN=![]() ﹣1,
﹣1,
由勾股定理得,FN2+MN2=MF2,
即(4﹣r)2+(![]() ﹣1)2=r2,
﹣1)2=r2,
解得r=![]() ,
,
②点P在点D的左边时,在Rt△MNF中,FN=r﹣4,MN=![]() +1,
+1,
由勾股定理得,FN2+MN2=MF2,
即(r﹣4)2+(![]() +1)2=r2,
+1)2=r2,
解得r=![]() ,
,
综上所述,⊙M的半径是![]() 或
或![]() .
.

 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=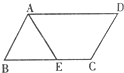 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.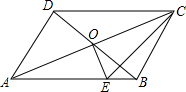 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是