题目内容
【题目】如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么 ![]() 的值是 .
的值是 . 
【答案】![]()
【解析】解:如图, 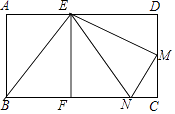
将△BEF绕着点E逆时针旋转得到△EMN,
∴BE=EN,EM=EF,MN=BF,
∵EF⊥BC,
∴BF=FN,
∴BF=FN=NM,
∵EF⊥BC,
∴四边形EFCD是矩形,
∴EF=CD,
∵点M恰好是边DC的中点,
∴DM= ![]() CD=
CD= ![]() EM,
EM,
∴∠DEM=30°,
∴∠DME=60°,
∵∠NME=90°,
∴∠CMN=30°,
设CN=x,
∴MN=2x,CM= ![]() x,
x,
∴CD=2 ![]() x,
x,
∴BF=FN=NM=2x,
∴BC=5x,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目